D'après l'étude précédente, on serait tenté de croire que le tenseur est suffisant pour représenter l'état de déformation d'un domaine matériel. En effet il permet de bien faire apparaître les différences entre les deux vecteurs et . Il semble même que la différence entre ces deux vecteurs soit à associer directement au champ de déplacement. En effet nous avons :                

On pourrait alors conclure que le tenseur gradient du champ de déplacement est le tenseur qui suffit à caractériser les déformations d'un domaine matériel. Cette conclusion est erronée, car il existe des cas de déplacement d'un domaine matériel qui respectent la notion de solides indéformables alors que le tenseur gradient du champ de déplacement est non nul. On peut par exemple imaginer le phénomène de rotation autour d'un axe. Il faut donc définir proprement un état de déformation.

Pour caractériser les déformations d'un domaine matériel, il faut en fait considérer les variations entre deux configurations de la distance existante initialement entre deux points matériels arbitraires. Hélas cette notion de distance n'est pas simple à mettre en œuvre et on préfère considérer les variations de deux vecteurs "matériels". Mathématiquement, cela revient à examiner les variations du produit scalaire de ces deux vecteurs. Un produit scalaire invariant quels que soient les deux vecteurs considérés est équivalent à une déformation nulle du milieu (pas de variation de longueur, pas de variation d'angle). On aura alors défini les changements de formes.

Imaginons deux vecteurs "matériels" et . Après transformation, nous obtenons les vecteurs et . Nous avons les relations :

        et   

Ce qui nous donne :

En utilisant les notations indicielles, nous obtenons :

La déformation locale est alors définie par le tenseur

On a ainsi :

avec    

. Ce tenseur peut être défini à partir du tenseur gradient du champ de déplacement :

La variation de notre produit scalaire devient alors :

Soit encore :

Nous obtenons ainsi un nouveau tenseur :

Ce tenseur est le tenseur des déformations de Green-Lagrange. C'est aussi un tenseur symétrique. On peut remarquer qu'il est identiquement nul dans un mouvement de corps solide . Ses composantes sont :

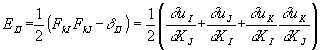
On dira que la déformation du système est homogène si le tenseur des déformations ne dépend pas des coordonnées spatiales de référence .

De la même façon que l'on définit le produit scalaire à partir du produit scalaire , on peut, de manière tout à fait symétrique, définir le produit scalaire à partir du produit scalaire .On aura alors les relations suivantes :

                Tenseur de Cauchy-Green gauche.

            Tenseur des déformations d'Euler-Almansi.

Le tenseur des déformations d'Euler-Almansi et le tenseur de Cauchy Green gauche sont des tenseurs eulériens, symétriques.

D'autre part, il est possible de démontrer la relation suivante :

Soit en composantes :