Comme nous venons de le voir, la caractérisation de l'état de déformation d'un domaine matériel passe par la détermination de tenseurs plus ou moins compliqués. Quel que soit le choix fait au niveau des tenseurs, on constate une non-linéarité provenant essentiellement des termes du type . Cette non-linéarité de l'état de déformation par rapport au champ de déplacement complique sérieusement les calculs.

Cependant, dans de nombreux cas, on pourra linéariser l'état de déformation en faisant l'hypothèse des transformations infinitésimales. Cette hypothèse, encore dénommée hypothèse des petites perturbations, se décompose en deux idées :

* Le déplacement de chacun des points du domaine matériel est petit. On pourra ainsi confondre l'état actuel avec l'état de référence.

* Le tenseur gradient de déformation ne contient que des termes négligeables devant l'unité.

Avec ces hypothèses, les différents tenseurs déformations deviennent :  

            Cauchy-Green droit

            Green-Lagrange

            Cauchy-Green gauche

            Euler-Almansi

On remarque donc qu'il y a une identification entre les descriptions lagrangienne et eulérienne.

Ainsi que nous l'avons déjà constaté, ce sont les tenseurs de déformation de Green-Lagrange et d'Euler-Almansi qui, plus que les tenseurs de déformation de Cauchy-Green, représente l'état de déformation en un point. En effet dans un déplacement de corps solide indéformable, les tenseurs de déformation de Green-Lagrange et d'Euler-Almansi sont nuls, alors que les tenseurs de déformation de Cauchy-Green sont confondus avec le tenseur identité.

On convient de dire que, dans le cas de petites perturbations, l'état de déformation est représenté par le tenseur des déformations linéarisé défini par :

Ce qui nous donne pour les coordonnées cartésiennes :

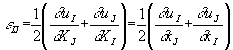
Ce nouveau tenseur est en fait la partie symétrique du tenseur gradient. Pour traiter de nombreuses applications, il peut être fait l'usage de la partie antisymétrique du tenseur gradient. Les relations sont les suivantes

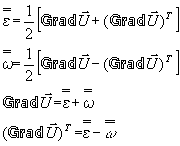
L’emploi du tenseur des déformations en lieu et place du tenseur de Green Lagrange ou du tenseur d’Euler Almansi est une simplification importante car on obtient une linéarisation des déformations vis à vis du champ de déplacement. En effet si l’on considère deux champs de déplacement et , on peut écrire :

Avec ce qui précède nous pouvons écrire :

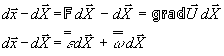
Supposons que représente, dans la configuration initiale, deux points et . Le vecteur représentera alors, dans la configuration actuelle les deux points et , transformé des deux points initiaux dans le champ de déplacement. On a alors les relations suivantes :

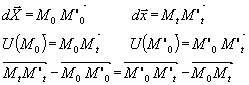
Ce qui nous permet d’écrire :

De plus, on peut montrer qu’à un tenseur antisymétrique du second ordre, il est possible d’associer un vecteur de tel sorte que l’on puisse remplacer le produit tensoriel par un produit vectoriel :

Ainsi , au voisinage du point , le champ de déplacement se présente sous la forme suivante :

Il existe malheureusement des cas d'études qui ne respectent pas l'hypothèse de petites perturbations.

On trouve en particulier le non-respect de cette hypothèse simplificatrice dans des opérations de mise en forme imposant à la fois de grands déplacements et de grandes déformations. Mais on peut aussi trouver des applications qui ne respectent pas que l'une des conditions. Ainsi, en robotique, on est souvent confronté à des problèmes de grands déplacements, mais dans chacun des éléments, on peut considérer que les déformations sont très faibles.

Ces hypothèses sont d'une réelle importance pour la simplification des calculs. Prenons par exemple le cas d'une poutre console encastrée en une section extrémité, libre à l'autre extrémité et supportant une charge uniformément répartie.

Déjà la définition rigoureuse de la charge pose un problème. Cette charge conserve-t-elle une direction constante qu'elle que soit la déformée de la poutre (cas de l'attraction gravitationnelle), ou bien cette charge est-elle suiveuse, c'est-à-dire, conserve-t-elle une direction fixe vis à vis de l'élément de poutre sur lequel est s'applique (cas d'une pression) ?  

La réponse à cette question étant trouvée, si on veut déterminer la déformée de notre poutre en utilisant la théorie classique des poutres, il convient de bien réaliser que, si cette déformée est grande, on a vite affaire à une poutre courbe. En conséquence la formule classique devra être délaissée au profit de la formule suivante qui fait apparaître le rayon de courbure de notre poutre initialement droite :

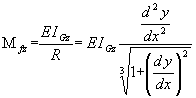
Bien entendu les problèmes d'intégration sont accrus. De plus le calcul du moment de flexion pose tout de suite plus de difficultés. En effet suivant que l’on prenne en compte ou non la rotation des sections, on constate qu’il y a une différence dans l’évaluation du bras de levier.