L’état de contrainte est donc représenté par un tenseur. Ainsi que nous l’avons déjà vu il est possible d’obtenir une représentation graphique plane par cercle de Mohr.

Dans le plan de cette représentation, on trace le lieu de l’extrémité du vecteur contrainte, en fonction de l’orientation de la normale à la facette choisie au point considéré. Si la normale appartient à un plan principal, ce lieu est l’un des trois cercles de Mohr associés aux plans principaux. Si la normale appartient à deux plans principaux, c’est à dire si la normale est confondue avec une direction, alors le vecteur contrainte est situé sur l’axe de la normale, l’extrémité du vecteur étant alors confondu avec le point commun aux deux cercles de Mohr. Enfin si la normale est quelconque dans l’espace des vecteurs propres, l’extrémité du vecteur contrainte se trouve à l’intérieur du tricercle.

L’avantage de cette représentation graphique réside dans la facilité de visualisation des composantes normales et tangentielles d’un vecteur contrainte. On vérifie aisément que la plus grande contrainte principale est en fait la valeur maximale de la contrainte normale en un point alors la valeur minimale est donnée par la plus petite contrainte principale. Pour ce qui est de la contrainte tangentielle, la plus grande valeur est donnée par la demi différence entre la plus grande contrainte principale et la plus petite contrainte principale. Elle est obtenue pour la direction de normale qui correspond à la bissectrice du plan principal associé à la contrainte principale maximale et la contrainte principale minimale.

Si on se donne la convention d’ordonner les contraintes principales selon une décroissance, on a :

Considérons une poutre droite de section circulaire sollicitée en flexion pure combinée avec de la torsion. On désigne par l’axe de la poutre (ligne des centres de gravité) et par l’axe du moment de flexion. Il est alors possible de démontrer que, dans le cadre des hypothèses de la théorie des poutres, les tenseurs contraintes associés à ces deux sollicitations sont dans la base cylindro polaire :

Pour la flexion : avec

Pour la torsion : avec

L’état de contrainte résultant est donc :

A partir de ce tenseur, il est simple de représenter le tricercle de Mohr. En effet, on constate aisément que le vecteur représente une direction principale, la contrainte principale associée étant nulle. Le plan est donc un plan principal de contraintes auquel il est possible d’associer un cercle de Mohr.

Pour la construction de ce cercle, il suffit de représenter quelques points appartenant à ce cercle, c’est à dire de définir l’extrémité de vecteur contrainte pour quelques directions de normales appartenant au plan principal. On peut alors choisir de représenter les vecteurs contraintes associés aux directions et . On a :

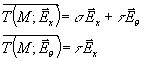
La construction du cercle de Mohr est alors possible et elle montre que les valeurs des contraintes principales sont :