Convention d'écriture
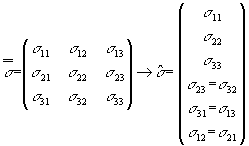
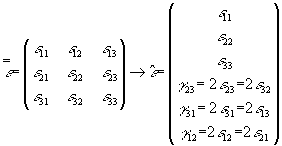
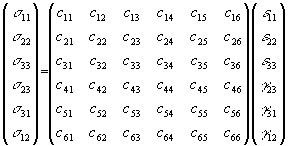
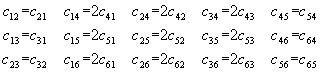
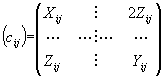
les matrices X et Y étant symétriques
21 coefficients indépendants
|
Isotropie
|
|
Convention d'écriture
|
|
|
|
|
|
|
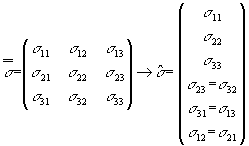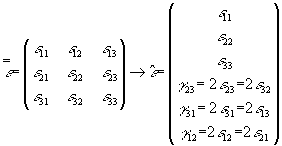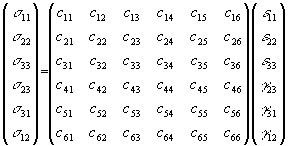| conditions d'intégrabilité de Cauchy |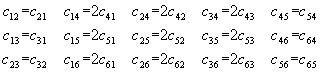
|
|
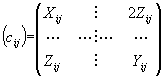les matrices X et Y étant symétriques 21 coefficients indépendants |
|
Hypothèses sur le degré d'anisotropie Symétries et rotations possibles sans changement de la loi de comportement Invariance par changement de bases
Tenseur d'ordre 2
Tenseur d'ordre 4
|
|
Matériau isotrope
|
|
La loi de comportement est indépendante du repère choisi pour l'exprimer
|
|
Les directions principales de contraintes sont confondues avec les directions principales de déformations |
|
Matériau orthotrope
|
|
invariance par changement de direction obtenue par symétrie relative à deux plans orthogonaux Exemples : le bois, les composites unidriectionnels, les produits métalliques laminés |
|
symétrie par rapport au plan de coordonnées
13 coefficients indépendants |
|
symétrie par rapport à un plan orthogonal
9 coefficients indépendants |
|
Dans le repère d'orthotropie
|
|
9 coefficients indépendants * 3 modules d'élasticité longitudinal
* 3 modules de cisaillement * 3 coefficients de contraction
|
|
considérations thermodynamiques sur le travail de déformation
|
|
Matériau isotrope transverse
|
|
invariance par changement de direction obtenue par rotation autour d'un axe privilégié donc orthotropie |
|
|
|
5 composantes indépendantes
|
dans les directions de l'orthotropie.
.
.
axe d'isotropie
