Les propriétés très générales de l'espace affine resteront évidemment valables lorsque nous choisirons une métrique, c'est à dire lorsque nous fixerons à tous les vecteurs de base une commune mesure. En partant d'un repère orthogonal, dont les vecteurs de base ont tous un même module, on peut construire une infinité d'autres repères rectilignes ou curvilignes, au moyen d'un changement de coordonnées, changement au cours duquel toute longueur doit rester invariable. La notion de longueur permettra ensuite de définir la notion d'angle.

Soit un espace vectoriel sur un corps K de scalaires. Nous allons enrichir sa structure et le rendre métrique en définissant une nouvelle loi de composition qui sera appelée la multiplication scalaire.

Toutes les multiplications scalaires ont un point commun : à tous couples de vecteurs de elles associent un produit scalaire qui donne un scalaire intrinsèque noté .

Le produit scalaire possède les 4 propriétés suivantes :

* commutativité de la multiplication scalaire

*associativité de la multiplication scalaire par un scalaire

*distributivité par rapport à l'addition       

*si pour tout , alors

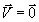
A partir de quatre axiomes, il est facile d'expliciter la multiplication scalaire. On associe une base à l'espace vectoriel . On peut alors écrire:

Ce qui nous donne pour l'expression de la multiplication scalaire :

Soit :

        avec

On remarque donc que tous les produits scalaires seront définis à partir des produits scalaires des vecteurs de base.

D'après la commutativité, on a nécessairement :

D'autre part, la quatrième propriété du produit scalaire nous permet d'écrire :

Autrement dit, le système des n équations aux n inconnues n'admet que la solution . Pour cela, il faut et il suffit que la matrice des soit régulière et que son déterminant soit non nul.

Réciproquement, si nous nous donnons arbitrairement scalaires tels que :

        et

il est immédiat de vérifier que la loi de multiplication définie par  pour et satisfait aux quatre axiomes.

En conclusion, il existe effectivement une loi de multiplication scalaire satisfaisant aux quatre propriétés. On peut se la définir en se donnant arbitrairement, pour une base , les produits scalaires :

        tels que et

Les sont les composantes deux fois covariantes d'un tenseur sur que nous noterons et que nous appelerons le tenseur fondamental sur .

On appelle forme bilinéaire fondamentale de l'expression explicite du produit scalaire du couple de vecteur générique.

On appelle forme quadratique fondamentale l'expression correspondante du carré scalaire de son vecteur générique :

Il est à noter qu'il suffit de se donner cette dernière forme pour définir complètement les et par conséquent la loi de composition scalaire sur .

Enfin, la matrice des étant régulière, elle est inversible et nous noterons les éléments symétriques de sa matrice inverse. Nous pourrons donc écrire :

Changement de bases

Considérons une nouvelle base . On peut bien entendu définir les produits scalaires des vecteurs de cette base :

Mais on peut aussi calculer ces produits scalaires en fonction des produits scalaires des vecteurs de la base et de la matrice de changement de base. Le résultat est :

De même pour le tenseur fondamental inverse, on a :

On peut aussi calculer le déterminant de la matrice des que l'on appellera le déterminant de tenseur fondamental :

Dans le changement de base caractérisé par une matrice de déterminant nous obtiendrons la formule suivante :

Ce déterminant n'est pas conservé dans le changement de base, mais son signe reste indépendant de la base.

Composantes covariantes d'un vecteur

Soit un vecteur générique de . Quand on forme ses produits scalaires avec les vecteurs de base, on obtient :

Cette dernière entité, que l'on notera , est appelée la composante covarainte du vecteur dans la base .

Tout vecteur de l'espace muni du produit scalaire peut être défini par ses composantes contravariantes (avec ) ou par ses composantes covariantes (avec ). Les liens existants sont :

        et

L'introduction des composantes covariantes permet de varier les expressions du produit scalaire de deux vecteurs :

Cette relation nous permet d'affirmer que la suite est tensorielle.

Composantes contravariantes d'une forme linéaire

De même que pour le vecteur, on peut considérer un élément générique de , c'est-à-dire une forme linéaire définie par :

Du fait de la tensorialité de la suite , le terme est un tenseur contravariant qui caractérise la forme linéaire.

Toute forme linéaire de l'espace muni du produit scalaire peut être définie par ses composantes covariantes (avec ) ou par ses composantes contravariantes . Les liens existants sont :

        et

On remarque donc la forte analogie existante entre les vecteurs, éléments de l'espace vectoriel , et les formes linéaires, éléments de l'espace vectoriel dual . Cette analogie permet aussi de réaliser les changements d'espace vectoriel. Ainsi les relations précédents permettent d'identifier la forme linéaire à un vecteur de composantes covariantes . On pourra ainsi écrire pour tout vecteur de :

Cette relation montre bien que l'on peut confondre le vecteur et l'application linéaire .Ainsi un élément d'une base doit pouvoir s'identifier à un élément d'une base et vice-versa. On a :

Ce qui nous donne les relations fondamentales suivantes :

        et

Composantes d'un tenseur

On peut dons constater la confusion entre l'espace vectoriel et son dual . On en déduit que tous le tenseurs du même ordre p sur ne forment plus qu'un espace vectoriel unique, dont tout élément peut être défini par des composantes de variances arbitraires. Ces tenseurs seront appelés tenseurs pré-euclidiens.

Ainsi nous avons pour un tenseur pré-euclidien d'ordre 3 :

Ce qui nous permet d'écrire :

De la même nous allons pouvoir écrire :

Mais ces relations sont encore valables pour le tenseur fondamental. On peut donc ainsi définir ses composantes mixtes :

Et ses composantes complètement contravariantes :

Ainsi, les ne sont autre que les composantes complètement contravariantes du tenseur fondamental lui-même.

On obtient donc une règle dite d'abaissement ou d'élévation d'indice.

Pour élever (resp. abaisser) un indice k, on le remplace par un indice muet h et on effectue le produit contracté par (resp. par ).

On peut ainsi remarquer qu'un tenseur pré-euclidien admet différents modes de représentation. Il est possible de regrouper tous les indices en position supérieure ce qui nous donnera alors l'expression contravariante du tenseur. L'expression covariante sera obtenue avec un tenseur ayant ses indices en position inférieur.

Opérations sur les tenseurs pré-euclidiens

La possibilité de déplacer les indices accroît le nombre des opérations possibles.

Ainsi l'égalité de deux tenseurs pourra se définir simplement à partir de l'instant où ils sont du même ordre. De même l'addition sera obtenue aussi sur des tenseurs de même ordre. Pour ce genre d'opération, il faut définir les deux tenseurs dans la même base. Les propriétés obtenues étant intrinsèques, elles seront vraies dans toutes autres bases, en particulier celle obtenue par déplacement vertical d'indice.

De la même, la multiplication tensorielle est compatible avec les déplacements verticaux d'indices.

Cette relation, symétrique vis-à-vis des deux vecteurs, est encore vérifiée si l'un ou l'autre des deux vecteurs est nul. Autrement, elle subsiste si on remplace un vecteur par un vecteur parallèle. On dit donc que l'orthogonalité de deux vecteurs non nuls dépend seulement de leur "direction".

Une base est dite orthogonale si chacun de ses vecteurs est orthogonal à tous les autres.

Il est toujours possible de déterminer une telle base. Le processus de recherche d'une base orthogonale est appeler orthogonalisation de l'espace vectoriel.

Dans une base orthogonale, le carré scalaire d'un vecteur quelconque ne présente que des termes carrés. En effet si est une base orthogonale, le tenseur fondamental associé défini par doit être tel que est nul si I est différent de J.

Ainsi dans la base orthogonale, la matrice du tenseur fondamental est réduite à une forme diagonale. Toutefois, à priori, les termes ne sont pas nécessairement tous positifs. En conséquence, il n'est pas toujours possible de donner une base orthonormée dans un espace vectoriel pré-euclidien.

Pour pouvoir toujours définir une base orthonormée, il suffit de modifier la quatrième propriété du produit scalaire:

        si pour tout , alors  

La nouvelle propriété à prendre en compte est la suivante :

        si alors

Avec cette nouvelle propriété, on dit que la forme quadratique fondamentale est définie positive, c'est-à-dire strictement positive pour tout vecteur non nul.

Norme d'un vecteur

A tout vecteur de on peut associer un scalaire positif appelé norme du vecteur et défini par la racine carrée de son carré scalaire :

       

Les propriétés essentielles de la norme sont les suivantes :

* Inégalité de Schwarz

L'égalité n'est obtenue que si les vecteurs sont parallèles.

* Inégalité triangulaire

L'égalité n'est obtenue que si les vecteurs sont parallèles et de même sens.

Bases orthonormées d'un espace vectoriel euclidien

Dans un espace vectoriel euclidien , on appelle vecteur unitaire out vecteur de norme égale à l'unité. Les bases formées de vecteurs unitaires et deux à deux orthogonaux prennent le nom de bases orthonormées.

Les bases orthonormées sont celles qui réduisent la matrice du tenseur fondamental à la matrice unité.

Dans un changement de bases orthonormées, la matrice de changement de base est telle que son inverse est égal à sa transposée. On dit alors que c'est une matrice unitaire. Le déterminant d'une telle matrice est égal à plus ou moins un.