Soit un espace vectoriel de dimension n sur un corps K de scalaires. Dans la suite du cours, nous considérerons que la dimension de est finie et que le corps K est commutatif.

Dans ce chapitre, nous supposerons que est doté simplement d'une structure affine. C'est-à-dire que, outre l'égalité, les seules relations envisagées entre les éléments de seront l'addition et la multiplication par un scalaire.

Soit une base de . Un vecteur quelconque de est alors une combinaison linéaire des vecteurs de la base :

Soit une nouvelle base de . On aura alors de nouvelles composantes pour :

D'autre part, la nouvelle base est reliée à l'ancienne par les formules de changement de base et la matrice A associée :

Ce qui nous donne :

Mais de plus la matrice de changement de base est inversible et on peut lui associer son inverse B :

On aura donc :

        et

Les formules précédentes amènent la remarque suivante :

Alors que la nouvelle base a été définie en fonction de l'ancienne à l'aide des éléments de la matrice A, les nouvelles composantes du vecteur s'expriment en fonction des anciennes à l'aide de la matrice inverse B.

On exprime ce fait en disant que les composantes d'un vecteur de sont contravariantes dans un changement de base sur cet espace. On dit qu'un vecteur de est un tenseur contravariant du premier ordre sur .

Remarque : Pour plus de clarté dans les formules, nous avons employé des lettres majuscules pour tout ce qui se rapporte au second système de coordonnée, même pour les indices. Il est évident que ce genre de notation ne pourra être maintenu dans la suite où nous pourrons être amené à considérer plusieurs changement de base consécutif.

Dans le chapitre portant les espaces vectoriels nous avons défini les applications linéaires.

Nous appellerons forme linéaire toute application linéaire de sur le corps des scalaires K.

Une telle forme linéaire est donc un opérateur du type :

La notion de linéarité imposant :

On obtient donc dans une base :

On constate que apparaît comme une combinaison linéaire des . Toutefois, d'après sa définition, l'expression représente un scalaire intrinsèque, c'est à dire indépendant de la base utilisée dans .

De fait, un changement de base nous conduit aux relations :

        avec

On obtient aussi :

Ces formules nous montrent que les coefficients de notre forme linéaire varient dans le même sens que les vecteurs de base dans un changement de base. Nous dirons qu'ils sont covariants dans un changement de base.

On peut remarquer la notation employée. Arbitrairement, les vecteurs de base sont notés avec des indices inférieurs. Les vecteurs contravariants ont donc des indices supérieurs, alors que les coefficients covariants sont notés aces des indices inférieurs. Ce type de notation est celui que nous allons employer dans la suite.

Considérons l'ensemble des formes linéaires sur . Nous admettons que muni des lois de composition suivantes, cet ensemble est un espace vectoriel :

Addition de deux formes linéaires

Produit d'une forme linéaire par un scalaire

On admet la notion d'égalité entre deux formes linéaires :   

On aura en particulier la forme nulle :

L'ensemble des formes linéaires sur K est un espace vectoriel appelé espace dual de et noté .

Recherche d'une base de

étant un espace vectoriel, on peut toujours définir une base de cet espace vectoriel. Toutefois nous allons rechercher une base particulière de présentant des propriétés simples et rendant les calculs plus commodes.

Considérons comme éléments particuliers de les n formes linéaires définies par :

On démontre sans difficulté que pour toute forme linéaire f on a :

De plus la suite est libre. De fait elle constitue une base de . Ce qui nous amène aux conclusions suivantes :

L'espace dual de a la même dimension que .

Il admet la base appelée base duale de la base de .

Les coefficients d'une forme linéaire f, relativement à la base de ne sont que les composantes de f suivant la base de .

En recherchant l'espace vectoriel dual de l'espace vectoriel , on obtient un espace vectoriel de dimension n qui par correspondance peut être assimilé à l'espace vectoriel lui-même. La dualité est une relation réciproque.

Dans la dualité, la covariance devient la contravariance si nous adoptons au lieu de comme espace initial. Il est alors évident que les notions de variance seront étroitement dépendantes de l'espace vectoriel initial.

Soient et deux espaces vectoriels, distincts ou non, de dimensions finies n et m sur le même corps commutatif K de scalaires.

On rappelle que l'ensemble des couples tels que et est noté En ´ E'm.

On appelle produit tensoriel de par et on le note, un troisième espace vectoriel de dimension nm sur le corps K  muni d'une application de dans satisfaisant aux propriétés ci-après :

* La multiplication tensorielle est distributive, à droite comme à gauche, par rapport à l'addition .

* La multiplication tensorielle est associative avec la multiplication par un scalaire.

* Si p vecteurs sont linéairement indépendants et si q vecteurs , les produits le sont aussi.

A partir d'une telle loi de composition, il est possible d'établir une table d'opération. Considérons [resp. ] une base de [resp. de ]. D'après la troisième propriété, on obtient une base de en formant les nm produits : avec i = 1,2, ... , n et j = 1,2, ... , m

Cette base est appelée base associée dans aux bases de et de .

L'élément générique de est défini par :

1- Avec les propriétés de définition, on peut dire que la multiplication tensorielle des éléments de par les éléments de est une application bilinéaire de dans.

Attention, il faut bien distinguer une application dans et non pas une application sur . En effet, dans le cas général on ne peut pas associer un couple de à tout élément de. Ceci nous conduirait à rechercher n+m inconnues par partir de nm équations .

Ainsi l'ensemble des produits n'est en général qu'une partie de. On dit que les sont les éléments décomposés de .

2- Le produit tensoriel de deux vecteurs n'est pas commutatif en général. Considérons en effet la multiplication tensorielle d'un élément de par un élément de . Il faut tout d'abord noter que le problème de la commutativité ne peut se poser que si les deux espaces sont identiques. Dans ce cas, le produit est distinct du produit puisque les deux éléments et appartiennent à une base de .

On remarque que la définition de la multiplication tensorielle permet un calcul en cascade. En effet la multiplication tensorielle de deux espaces vectoriels et nous donne un troisième espace vectoriel . Ce dernier peut à nouveau servir à la définition d'un espace vectoriel à partir d'un espace vectoriel .

On imagine aisément la généralisation qui peut être faite.

Toutefois, afin d'éviter des difficultés complémentaires, nous imposerons une quatrième propriété à la multiplication tensorielle.

La multiplication tensorielle des éléments de plusieurs espaces vectoriels est associative.

Pour assurer cette associativité, il suffit de se l'imposer sur les vecteurs de base.

On peut donc maintenant donner une définition générale des tenseurs.

Nous appellerons tenseurs sur , tout élément de l'espace vectoriel .

L'expression générale de ces tenseurs est donc :

Les termes représentent les composantes de suivant la base . Il est évident que ces composantes sont fonctions des bases.

Considérons les changements de base suivants :

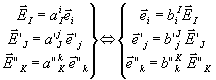
Dans la nouvelle base, les composantes du tenseur sont définies par la notion d'invariance de ce tenseur dans tous changement de base :

On peut alors en déduire les relations fondamentales suivantes :

En fait, en général, les tenseurs employés sont plus restrictifs car ils ne sont définis qu'à partir d'un espace vectoriel et de son dual .

On appelle tenseur d'ordre p sur tout tenseur sur un produit de p espaces vectoriels dont chacun est identique à ou à son dual .

Ce tenseur est dit affine si l'espace vectoriel est dotée d'une structure affine.

Les conventions de notation pour un tenseur de l'espace vectoriel sont les suivantes :

- Tous les facteurs du produit seront rapportés à une même base .

- Tous les facteurs du produit seront rapportés à une même base duale .

Ainsi à toute base de correspond une base de . Nous dirons que les composantes de suivant cette base sont les composantes de suivant la base .

Ces composantes seront notées . Un indice supérieur (resp. inférieur) correspondra donc à chaque facteur de base pris dans (resp. ) et les rangs latéraux des indices reproduiront l'ordre des facteurs de base correspondants.

Exemples

1- Considérons que soit en fait . L'ensemble des formes linéaires sur est l'espace vectoriel dual . Avec une seule multiplication tensorielle, nous pouvons faire apparaître quatre espaces vectoriels dont la dimension est 9 :

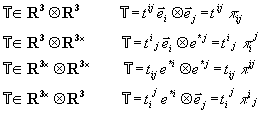
2- Un élément de sera noté :

Changement de base

Un changement de base est défini par les relations suivantes :

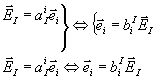
Dans l'exemple ci-dessus, les nouvelles composantes du tenseur sont :

Ce qui nous donne :

Les formules précédentes montrent bien l'intérêt d'une notation qui de prime abord semble un peu lourde.

Réciprocité

Inversement donnons-nous à priori une suite de composantes de .

Nous dirons que cette suite est tensorielle sur si ce sont les composantes d'un tenseur, autrement dit si est un élément intrinsèque de .

En fait, on peut traduire la tensorialité par l'affirmation suivante :

Pour qu'une suite de composantes de soit tensorielle sur cet espace, il faut et il suffit que le changement de base la transforme en une suite telle que :

       

On peut donc remarquer qu'il existe une correspondance biunivoque entre les tenseurs sur et les suites tensorielles sur cet espace. Pratiquement nous ne distinguerons pas le tenseur de la suite tensorielle et on notera en sous-entendant la référence à la base .

1- Tenseur de KRONECKER

Noté ou encore (et donc tout simplement ), le symbole de KRONECKER est tensoriel sur tout espace vectoriel . Le tenseur associé dont les composantes suivant une base particulière sont , est très caractéristique car les composantes sont indépendantes de la base utilisée. En effet, dans une autre base , les composantes de ce tenseur sont :

2- Attention, noté ou encore , le symbole de KRONECKER n'est pas tensoriel.

3- Dans le même ordre d'idée, il faut noter que les coefficients d'un changement de base ne sont pas tensoriels. La première caractéristique d'une suite tensorielle est de n'être fonction que d'une seule base. La suite est fonction du couple de base .

4- Considérons la suite des neuf produits scalaires des vecteurs de la base de :

Cette suite est symétrique car on a :

Cette suite tensorielle constitue la suite des composantes d'un tenseur appartenant à appelé le tenseur fondamental sur .

En géométrie, son importance est capitale, car la connaissance des neuf produits scalaires détermine les longueurs des vecteurs de base et les angles qu'ils font deux à deux.

Si on admet que le produit scalaire est une forme linéaire sur , on peut alors introduire les composantes covariantes des vecteurs de . Elles sont définies par :

On peut alors exprimer le produit scalaire de deux vecteurs quelconques :

Ainsi, pour obtenir le produit scalaire de deux vecteurs, il suffit de multiplier les composantes covariantes d'un vecteur par les composantes contravariantes de l'autre vecteur et de faire la somme de ces produits.

5- Un tenseur d'ordre p sur est apparu comme défini par une suite de composantes. En étendant cette notion à p=0, on obtient un être à une seule composante, sans variance, qu'on appelle un scalaire intrinsèque.

Pour la généralité de certains énoncés, il sera effectivement utile d'assimiler les scalaires intrinsèques aux tenseurs d'ordre 0.

On remarque, sur un tenseur d'ordre deux, que l'égalité avec est invariante pour tout changement de base. C'est une propriété intrinsèque à la suite tensorielle.

Si , on dit que le tenseur est symétrique et si on dit que le tenseur est antisymétrique.

Ces notions de symétrie et d'antisymétrie peuvent être généralisées à des tenseurs d'ordre supérieur à deux. L'observation vaut alors pour des symétries ou des antisymétries partielles, c'est à dire portant sur la transposition de deux indices particuliers, pourvu que ces deux indices soient à la même hauteur.

Ainsi le tenseur suivant est symétrique

En particulier, si un tenseur est complètement contravariant (ou complètement covariant), il se peut que toute transposition de deux indices change la composante correspondante en elle-même (resp. en son opposée). On dira alors que le tenseur est complètement symétrique (resp. complètement antisymétrique).