La loi de comportement que nous venons de définir admet malheureusement des limites. Dans pratiquement toutes les expériences, on constate en effet que, lorsque les efforts appliqués sont trop grands, le matériau perd ses qualités d’élasticité et qu’il subsiste des déformations permanentes appelées déformations plastiques. L’ingénieur est alors soumis à deux contradictions : assurer un prix de revient minimal, c’est à dire employer le moins de matière possible, et définir une structure performante et résistante, c’est à dire utilisant beaucoup de matière. Il est donc nécessaire pour lui de se trouver constamment à la frontière entre ces deux contraintes et pour cela il lui faut donc avoir les éléments qui définissent cette frontière.

La connaissance d’un état limite se détermine par les essais effectués en laboratoire. Il est logique de penser que cet état limite est lié au tenseur des contraintes car c’est l’expression tensorielle qui traduit la répartition des efforts à l’intérieur de la matière. En vertu de l’hypothèse d’isotropie du matériau, il est logique de penser que la limite élastique sera reliée aux valeurs propres de l’état de contrainte, c’est à dire aux contraintes principales. De plus il faut pouvoir tenir compte des différents résultats obtenus lors des essais expérimentaux.

Nous pouvons donc envisager la forme générale d’un critère comme étant une relation du type :

Dans cette expression, les coefficients permettent de prendre en compte les différents résultats expérimentaux. On supposera que les contraintes principales sont ordonnées :

Tout état de contrainte élastique vérifie l’inégalité, l’égalité étant obtenu en limite d’élasticité.

Afin de bien se représenter cette limite élastique, on peut envisager une représentation graphique. Pour cela on peut penser que le plan des cercles de Mohr, plan qui contient toutes les informations sur l’état de contrainte, doit convenir. On va donc commencer par représenter dans ce plan les différents résultats expérimentaux.

Traction unixiale

Parfaitement normalisé, c’est l’essai le plus couramment pratiqué. Sa mise en œuvre est relativement simple à condition de bien respecter le processus opératoire. L’essai de traction est aussi beaucoup utilisé pour définir les constantes élastiques du matériau. On démontre que, en des points au centre de l’éprouvette, l’état de contrainte est de la forme :

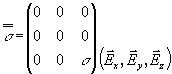
        représente l’axe de la poutre.

Nous sommes donc dans les directions principales et le tricercle de Mohr associé est de la forme :

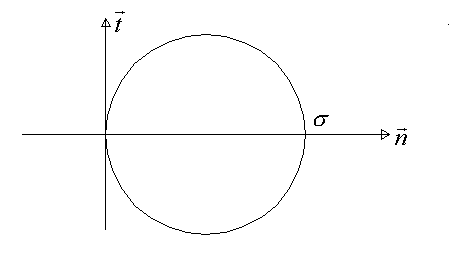
Les essais montrent que l’on est dans le domaine de comportement élastique tant que l’on vérifie la relation :

On définit ainsi la limite élastique en traction du matériau .

C’est un essai plus difficile à mettre en œuvre. Pour éviter les phénomènes de bord (frottement entre la pièce et les plateaux de compression) il faut une pièce élancée, mais on risque alors le flambement.

En des points au centre de la pièce l’état de contrainte est de la forme :

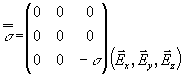        avec , contrainte normale de compression

Le tricercle de Mohr prend alors la forme suivante :

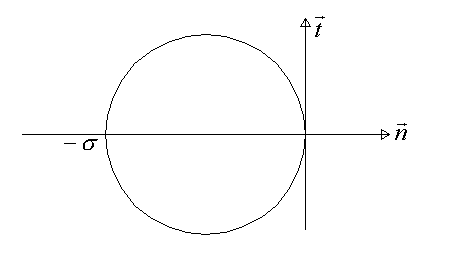
Les essais montrent que l’on est dans le domaine de comportement élastique tant que l’on vérifie la relation :

On définit ainsi la limite élastique en compression du matériau .

Cet état peut être obtenu dans le cas de la torsion d’un tube de faible épaisseur. Bien entendu nous sommes à nouveau confrontés à des problèmes de flambement. C’est pourquoi nous utilisons souvent l’essai de torsion sur des poutres droites circulaires à section pleine. L’état de contrainte est de la forme :

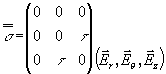
Après calcul des valeurs propres , il est facile de représenter le tricercle de Mohr :

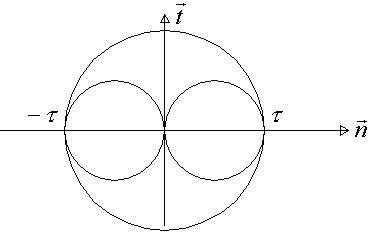
L’expérience montre qu’il existe une valeur de contrainte tangentielle à ne pas dépasser si l’on veut rester dans un état élastique :

C’est en fait le cas d’un corps auquel on applique une pression uniforme sur sa surface. L’état de contrainte est alors sphérique est on a :

L’expérience montre qu’en fait il n’y a pratiquement pas de limite à la valeur de la pression appliquée. Après retour à un état de pression nulle, le corps retrouve intégralement sa forme initiale : il n’y a aucune déformation permanente.

La détermination d’un critère est particulièrement délicate. Il n’existe malheureusement pas de critère universel qui intègre tous les résultats expérimentaux. Même si il était possible de déterminer un tel critère, il est à craindre que le coût d’établissement et le coût d’utilisation ne seraient pas admissibles industriellement. En effet la détermination des différentes limites élastiques associées aux différents essais fait appel à des machines d’essai plus ou moins sophistiquées qui peuvent être onéreuses. Aussi on préfère utilisé des critères qui ne font appel qu’à un ou deux essais et qui sont plus simples à mettre en œuvre. On est alors parfaitement conscient que l’on perd de la précision, mais il faut relativiser cette perte vis à vis des incertitudes de mesures expérimentales des limites élastiques, ou de détermination des grandeurs caractéristiques de la loi de comportement.

Le critère de Von Misès

Ce critère est basé sur le dernier constat concernant la compression isotrope et sur l’énergie de déformation. Comme il n’y a aucune limite, il faut que ce critère permette de quantifier une énergie de déformation qui ne dépende pas de la compression isotrope.

En se basant sur les résultats obtenus par l’expérience, à savoir que l’on modifie le volume sans modifier la forme, on peut montrer que le tenseur des contraintes, comme le tenseur des déformations, est purement sphérique. Les parties déviatoriques sont nulles.

L’idée associée au critère de Von Misès est donc de limiter l’énergie de déformation élastique déviatorique, c’est à dire celle obtenue à partir des tenseurs déviateurs.

On a vu que l’énergie de déformation avait l’expression infinitésimale suivante :   

Avec une loi de comportement élastique linéaire on obtient :

Avec la décomposition en partie sphérique et déviatorique, on obtient :

Pour le critère de Von Misès on a :

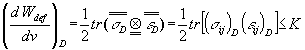
En tenant compte des résultats donnés par l’essai de traction et en exprimant l’énergie de déformation déviatorique en fonction de l’état de contrainte, on obtient :

En fonction des contraintes principales on a :

Ce critère, qui vérifie particulièrement bien le cas de la compression hydrostatique, présente l’inconvénient d’être symétrique en traction et en compression. Il ne permet pas de prendre en compte une différence entre la limite élastique en traction et la limite élastique en compression. Son principal intérêt réside dans sa simplicité d’usage.

Le critère de Tresca

Ce critère est basé sur une limitation du cisaillement en un point. Il revient en fait à limiter le rayon du plus grand des cercles de Mohr et de ce fait il est particulièrement bien adapté à des sollicitations de cisaillement comme la torsion d’une poutre.

Son expression est simplement donné en contraintes principales ordonnéespar la formule :

Comme pour le critère de Von Misès, on se trouve devant un critère simple à définir et à mettre en œuvre mais qui ne permet pas de prendre en compte la complexité des différents résultats d’essais. En particulier, comme pour le critère précédent, on constate qu’il n’y a aucune limitation à une sollicitation de traction isotrope, ce qui va à l’encontre des résultats expérimentaux.