A ces trois lois, il faut impérativement ajouter la loi de conservation de la masse. Souvent, en mécanique, on oublie de traduire le fait que le domaine étudié ne transforme pas sa masse dans son mouvement. Cela provient du fait que l’enseignement traditionnel de la mécanique du solide se fait en variables de Lagrange et que l’on suit la particule (ou le domaine) dans son mouvement. Par contre, en variables d’Euler, il faut bien traduire le fait qu’il n’y a pas de transformation de la masse du milieu étudié même si localement il peut y avoir une modification de la masse volumique.

Ainsi que nous allons le constater, ces lois peuvent s’exprimer soit sous forme globale, c’est à dire écrite pour un domaine matériel, soit sous forme locale, c’est à dire en équation différentielle valable en chaque point du domaine.

Avant de donner des expressions d’une loi de conservation, il convient de compléter le bagage mathématique en précisant la notion de dérivée particulaire d’une intégrale de volume et les énoncés de deux théorèmes importants, le théorème de la divergence et le théorème de l’intégrale nulle.

Soit un domaine que l’on suit dans son mouvement et considérons la variation entre deux instants infiniment proche de l’intégrale d’un champ tensoriel volumique sur le domaine :

Cette variation est due à deux contributions, d’une part la variation propre du champ tensoriel entre les deux instants et d’autre part la variation du domaine entre les deux instants.

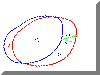
Pour calculer l’expression totale, désignons par le domaine à l’instant t et par le domaine à l’instant t+dt. L’instant les séparants étant infiniment petit, on peut supposer qu’ils possèdent une large intersection commune que l’on désignera par .

Ainsi le domaine à l’instant t se décompose en deux sous domaines, l’intersection commune et la perte de domaine , alors que le domaine à l’instant t+dt se décompose en et le gain de domaine .

On peut écrire :

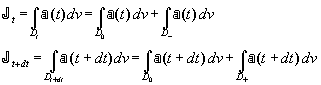
On peut alors calculer la variation :

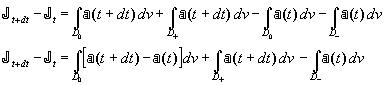
Mais pour les domaines et , l’accroissement et la diminution de volume sont dus au déplacement de la surface génératrice. On peut donc écrire :

        Pour        

        Pour        

L’intervalle de temps étant infiniment court, on a alors :

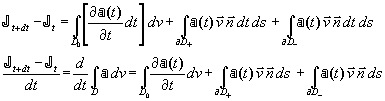
Dans ces expressions, (resp. ) représente la surface commune aux domaines et (resp. ). On peut donc en déduire la relation fondamentale suivante :

.

Nous nous contenterons de donner, sans démonstration, un énoncé de ce théorème appelé aussi théorème de Green – Ostrogradski :

Le flux d’un champ tensoriel au travers de la surface enveloppant le domaine est égal à l’intégrale de la divergence du champ tensoriel sur le domaine :

Remarques :

Dans le cas où représente un champ vectoriel constant, on obtient

                    Dans le cas où représente un champ scalaire , on obtient

L’énoncé de ce théorème est le suivant :

Considérons un champ vectoriel volumiquedéfini et continu sur un domaine . Si quelque soit le sous domaine inclus dans , l’intégrale du champ tensoriel sur le domaine est nulle, alors le champ tensoriel est identiquement nul.

Pour la démonstration de ce théorème, il suffit d’imaginer que le champ tensoriel n’est pas nul en un point donné du domaine . Du fait de la continuité, il est alors possible de définir un domaine infiniment petit enveloppant le point et tel que l’intégrale du champ tensoriel ne soit pas nul, ce qui va à l’encontre de l’hypothèse de départ.

On peut dire que d’une manière générale, une loi de conservation exprime un bilan d’une grandeur tensorielle . On peut alors associer à cette grandeur :

        La densité volumique dans le domaine considéré :

        La densité volumique produite par unité de temps dans le domaine considéré :

        La densité surfacique associée au flux de entrant à travers de la frontière du domaine :

La loi de conservation a alors comme expression générale :

Equation qui traduit le fait que la variation de la grandeur au cours de l’intervalle de temps dt est égale à la somme de la quantité produite (algébriquement) à l’intérieur du domaine et de la quantité entrant (algébriquement) à travers la frontière du domaine.

Le principe de conservation de la masse postule qu’il n’y a ni apparition ni disparition de matière. En conséquence la variation de la masse au cour du temps est nulle :

La masse peut se calculer à partir de la masse volumique :

Avec la notion de dérivée particulaire d’une intégrale de volume, on obtient :

On peut encore utiliser le théorème de la divergence :

Ce qui nous donne une forme locale de l’équation de continuité avec le théorème de l’intégrale nulle :

De plus nous avons les relations :

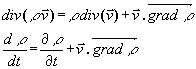
On obtient ainsi une autre forme locale de l’équation de continuité :