Le tenseur de raideur est un tenseur d'ordre 4. Il est donc particulièrement délicat à expliciter. Les formules développées sont relativement lourdes. Il convient donc de trouver une méthode qui permette une simplification d'écriture.

La solution réside en des applications linéaires. L'une va nous permettre de passer de l'espace vectoriel de dimension 2 associé aux tenseurs d'ordre 2 vers un espace vectoriel de dimension 1 auquel on associera des tenseurs d'ordre 1. Pour le tenseur des contraintes, cette application se présente sous la forme suivante :

Par contre pour le tenseur des déformations, on préfère utiliser l'application définie par :

Ces transformations sur les tenseurs des contraintes et des déformations induisent l'existence d'une application linéaire de l'espace vectoriel de dimension 4 (associé au tenseur de raideur) vers un espace vectoriel de dimension 2 :

La nouvelle forme du tenseur de raideur permet alors de lui associer une matrice carrée (6,6) :

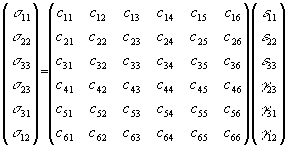
Compte tenu des conditions d'intégrabilité de Cauchy sur le travail de déformation, nous avons les relations suivantes :

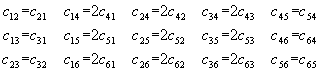
Ces relations étant au nombre de 15, nous nous retrouvons bien avec 21 coefficients indépendants.

La structure de la matrice C devient alors :

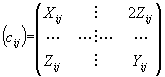
Les sous-matrices X, Y et Z étant des matrices (3,3), les matrices X et Y étant symétriques.

Les hypothèses supplémentaires portant sur le degré d'anisotropie du matériau vont nous permettent de diminuer le nombre des coefficients indépendants.

Ces hypothèse portent essentiellement sur les symétries et rotations possibles sans changement de la loi de comportement. L'invariance du comportement dans un certain type de changement de base ne sera en effet vérifié qu'avec des relations particulières du tenseur de raideur.

Pour mettre en évidence ces relations on rappelle les règles de transformation des composantes d'un tenseur dans un changement de bases orthonormées :

Pour un tenseur d'ordre 2, on a :

Pour un tenseur d'ordre 4, on obtient :

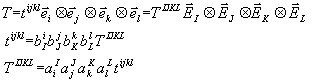
Remarque La notation précédente (avec des indices supérieurs et inférieurs) peut choquer à première vue mais cette notation est en conformité avec les notions de variance et de contravariance. Elle permet des écritures avec des simplifications systématiques. De plus, dans le cas d'une métrique non euclidienne, elle seule permettra de prendre en compte correctement les nouvelles notions de longueur.

Toutefois, dans un souci de simplicité, nous continuerons à utiliser des notations avec des indices inférieurs pour les tenseurs.

L'hypothèse d'isotropie impose que la loi de comportement soit indépendante du repère choisi pour l'exprimer. En d'autre terme, le tenseur de raideur doit être invariant pour tout changement de base. On peut alors démontrer que la seule forme possible de ce tenseur est :

On obtient ainsi la loi de comportement faisant apparaître les coefficients de Lamé :

Avec cette forme de relation, on constate que les directions principales de contraintes sont confondues avec les directions principales de déformations.

Cette loi de comportement fera l’objet d’une étude approfondie dans la suite du cours.

Un milieu est dit orthotrope pour une propriété donnée si cette propriété est invariante par changement de direction obtenue par symétrie relative à deux plans orthogonaux.

On remarque qu'alors la symétrie par rapport au troisième plan orthogonal est automatiquement acquise.

Ce mode de comportement est relativement bien réalisé pour le bois (dans certains cas), les composites unidirectionnels et les produits métalliques laminés.

Supposons que nous ayons une symétrie par rapport au plan de coordonnées . La matrice de changement de base traduisant cette symétrie est :

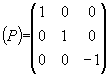
La relation d'indépendance du tenseur de raideur dans ce changement va se traduire par le fait que toutes les composantes ayant un nombre impair d'indice 3 sont nulles. Ainsi pour la matrice C on obtient :

Le tenseur de raideur n'a plus que 13 coefficients indépendants.

Il nous reste maintenant à traduire la condition de symétrie par rapport à un plan orthogonal, par exemple celui de coordonnées . On aura donc :

Il ne reste donc que 9 coefficients indépendants pour traduire le comportement de notre matériau. Dans le repère principal d'orthotropie, la loi peut se mettre sous la forme :

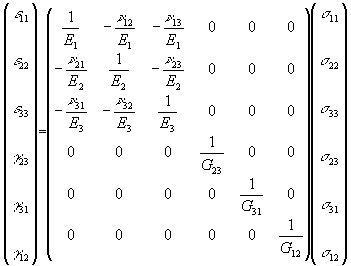
Les conditions de symétrie se traduisent par les relations :

Le matériau est donc caractérisé par 9 coefficients indépendants :

* 3 modules d'élasticité longitudinal dans les directions de l'orthotropie.

* 3 modules de cisaillement .

* 3 coefficients de contraction .

De plus, des considérations thermodynamiques sur le travail de déformation permettent de démontrer les inégalités suivantes :

Un milieu est dit isotrope transverse pour une propriété donnée si cette propriété est invariante par changement de direction obtenue par rotation autour d'un axe privilégié. Dans ce cas, tout plan passant par l'axe privilégié est un plan de symétrie. Nous pouvons donc remarquer que le milieu est déjà orthotrope.

Imaginons par exemple que l'axe soit l'axe d'isotropie. Il est donc nécessaire d'avoir une invariance de la loi de comportement pour toute rotation définie par :

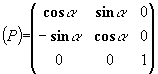
On conçoit facilement qu'en plus des relations du cas orthotrope, on obtienne de nouvelles relations entre les coefficients élastiques du tenseur de raideur. On aura par exemple :

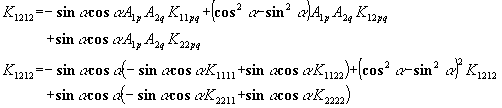
Ce qui nous donnera :

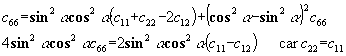
D'où la relation :

En définitive on retrouvera 4 nouvelles équations (dont ). Il n'y a donc plus que 5 composantes indépendantes. Les équations deviennent :

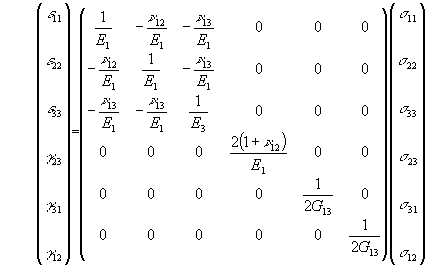
        Les 4 relations supplémentaires étant :