OBJECTIF

RESUME

1.   INTRODUCTION

2.   VOILEMENT

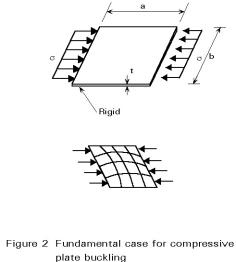
Le voilement d'une plaque a lieu lorsque sa section à âme mince subit des contraintes de compression. Ce phénomène ressemble assez au flambement de poteau ; il implique cependant plutôt les éléments de la section droite du composant que le déplacement de la section dans son ensemble.

Les sections formées à froid et les sections constituées de plaques minces sont les plus sensibles au voilement.

Les modes de flambement élastique et les contraintes critiques correspondantes des plaques en compression dérivent des équations des plaques faiblement déformées .

La résistance postflambement apparaît en particulier sur les plaques qui ont des proportions réduites et qui, jusqu'à une certaine limite, se comportent de manière élastique. Dans ce cas, la charge ultime peut être égale à plusieurs fois la charge critique élastique. Pour des plaques d'élancement faible ou intermédiaire, c'est la plasticité du matériau qui affecte principalement le comportement de la plaque ; en fait plus la plaque est massive, plus l'écoulement plastique aura tendance à précéder le voilement, ce qui donnera lieu à une résistance ultime éventuellement plus faible que la charge critique élastique.

Les processus de mise en œuvre et de fabrication d'une plaque donnent lieu à des imperfections géométriques inévitables et à des contraintes résiduelles. Dans la plupart des cas, les deux ont des effets sur le comportement pré- et postflambement.

L'élancement de la plaque est le paramètre géométrique qui gouverne la résistance ultime de la plaque. Cette dernière est généralement représentée (figure 6a), par le tracé de la contrainte principale appliquée à l'effondrement par rapport au paramètre d'élancement l' = b/t, « b » désignant l'épaisseur de la plaque dans la direction perpendiculaire à la compression. Une plaque élastique initialement plate flambe pour une contrainte critique :

où :       n            est le coefficient de Poisson 

k_s       désigne le coefficient de voilement             

À cause de la plasticité du matériau, la charge d'écrasement fournit une limite à la résistance de la plaque et constitue une limite tronquée de la courbe de flambement élastique. La transition entre l'écrasement et le voilement a lieu pour s_cr = f_y, c'est-à-dire pour la valeur suivante de l'élancement :

De la même manière que pour les courbes de résistance des poteaux, les courbes de résistance des plaques sont d'habitude tracées selon des coordonnées normées (figure 6b) : la contrainte ultime principale est divisée par la contrainte d'élasticité du matériau, tandis que l'on définit un élancement normé de la plaque, comme pour le flambement de poteau, dans les termes généraux :

En utilisant l'équation (1), l'élancement normé de la plaque est :

En conséquence,  constitue l'élancement limite correspondant à la transition entre l'écrasement et le voilement.

3.   FLAMBEMENT DES POTEAUX PAR TORSION

Comme pour le flambement par flexion, on doit aussi tenir compte des imperfections géométriques, des contraintes résiduelles et des effets dus à la plasticité du matériau et à l'écrouissage. En ce qui concerne les imperfections géométriques initiales, la rotation initiale du barreau et le manque de planéité des composants de la section sont, comme on peut le comprendre, les plus significatifs. A la différence du flambement par flexion, pour lequel on a beaucoup d'informations, la résistance ultime associée au flambement par torsion ne peut pas être estimée avec une grande précision à cause du manque d'expériences suffisamment documentées et des résultats correspondants des tests. On accepte généralement que la procédure utilisée pour le flambement par flexion puisse être étendue au flambement par torsion, sous réserve de faire l'hypothèse que les diminutions de résistance dues aux imperfections et à la plasticité sont semblables dans les deux cas, si on les exprime en coordonnées normées. L'élancement normé est logiquement défini de la manière suivante :

4.   FLAMBEMENT PAR FLEXION-TORSION

Les déplacements de flexion et de torsion se combinent quand le centre de cisaillement et le centre de gravité de la section ne correspondent pas. Ceci a pour conséquence une réduction de la charge critique de flambement par rapport à celle du flambement par flexion.

Pour illustrer cette forme de flambement, on considère une section en U soumise à une charge de compression uniaxiale appliquée au centre de gravité, de telle sorte que les sections terminales subissent une contrainte uniformément appliquée. Dès que le barreau a tendance à flamber dans la direction yy, c'est-à-dire par flexion par rapport à l'axe zz, la flèche v(x) crée un moment de flexion M(x) = Nv(x), donnant naissance à un cisaillement correspondant :

                       V = dM/dx = N(dv(x)/dx).

Tout se passe comme si le barreau était soumis à des forces distribuées transversales :

                                                  q = - dV(x)/dx = - N (d²v(x)/dx²)

agissant dans le plan yy contenant le centre de gravité G et non pas dans le plan zz qui contient le centre de cisaillement C (figure 9c). De ce fait, la flexion par rapport à l'axe zz et le cisaillement correspondant induisent un moment de torsion dM_t = qz_odx, où z_o représente la distance entre le centre de gravité et le centre de cisaillement. Ceci veut dire qu'un flambement purement par flexion dans le plan yy est impossible, parce que les déformations de flexion et de torsion sont inévitablement couplées.

Le flambement par flexion-torsion est déterminé par trois équations différentielles d'équilibre qui contiennent les dérivées des trois fonctions : déplacements v et w dans les plans yy et zz et la rotation y.

Dans le cas usuel du barreau biarticulé, parfaitement libre de se gauchir, c'est-à-dire v = v" = 0, w = w" = 0 et y = y" = 0 aux extrémités, la contrainte critique de flambement par flexion-torsion vaut :

où           y_o et z_o    sont les coordonnées du centre de cisaillement, avec .

Il faut noter que pour une section doublement symétrique (z_o = y_o = r_o = 0), les racines sont :

et que la plus faible de ces trois valeurs - s_cr,T, s_cr,zz et s_cr,yy - est celle qui est déterminante.

Le flambement par flexion-torsion entraîne des déformations dues à la fois au flambement du poteau par flexion et par torsion. La résistance ultime associée sera alors modifiée par tous les types d'imperfections, dans la mesure où elles modifient ces deux phénomènes de base.

Comme dans le cas du flambement de poteau en torsion, on manque d'information sur la perte de résistance de flambement par flexion-torsion due aux imperfections, aux contraintes résiduelles et à la plasticité du matériau ; ici encore, on peut généraliser la procédure utilisée pour le flambement par flexion en utilisant les mêmes courbes de résistance normée, en supposant que l'élancement normé est défini de la manière suivante :

5.   DEVERSEMENT DES POUTRES

Pour une poutre parfaite, chargée dans la direction de la flexion la plus forte, le déversement se produit pour une valeur critique du moment fléchissant maximum ou de la contrainte de compression maximum. Cette valeur dépend de plusieurs facteurs : la distribution de moment le long de la poutre (forme du diagramme de moment fléchissant), les conditions aux limites (maintiens en flexion, torsion et gauchissement), le niveau d'application des charges transversales et la possible dissymétrie de la section droite. Comme ce flambement mêle torsion et flexion selon l'axe le plus faible, le moment fléchissant critique pourra s'exprimer en termes de longueur de poutre L, de rigidités en torsion et vis-à-vis du gauchissement, respectivement G I_t et E I_w et en termes de rigidité de flexion par rapport à l'axe le plus faible, E I_zz.

Le moment fléchissant critique élastique d'une section en I ou H, par exemple, est donné par :

où           C₁ et C₂ sont des coefficients qui tiennent compte de l'influence des facteurs mentionnés ci-dessus,              

         est la distance du centre de cisaillement au point d'application des charges transversales.

La contrainte de déversement critique élastique vaut :

En plus de la plasticité du matériau et des contraintes résiduelles, les imperfections géométriques créent une perte de résistance par rapport à la charge critique élastique. On doit faire attention à toute imperfection capable de déclencher de la torsion et/ou de la flexion latérale. Une récente évaluation statistique de résultats de tests, mis en oeuvre pour préparer les documents de fond de l'Eurocode 3 a montré que la forme des courbes de résistance ultime pour le flambement des poteaux par flexion est tout à fait appropriée à la représentation de la réponse en déversement, à condition de calibrer correctement les paramètres de la courbe. Comme pour les formes précédentes de flambement, l'élancement normé de déversement est défini par :

6.   FLAMBEMENT DES COQUES

Le cas le plus simple à analyser est celui de la coque cylindrique chargée axialement; la contrainte critique de flambement élastique est donnée par :               

t             épaisseur de l'âme

r             rayon du cylindre

Même de très faibles imperfections géométriques créent un écart prématuré de la courbe effort-déplacement de la coque parfaite donnant couramment une réduction significative de la capacité de résistance à la charge (figure 12). Les coques réelles ne peuvent donc pas atteindre la charge critique élastique. L'influence des imperfections sur la charge ultime des coques est un problème très complexe qui a fait l'objet de recherches importantes.

L'influence des différents types d'imperfections sur la résistance ultime peut varier de façon importante selon le type de coque et le type de chargement. On peut définir une courbe de résistance normée en représentant le rapport s/f_y par rapport à l'élancement normé , de façon analogue à l'approche utilisée pour les courbes relatives à la résistance des poteaux et des plaques.

Il faut noter que, si  augmente, la courbe de résistance s'approche de la valeur critique de la résistance (réduite par le facteur a).

7.   AMELIORATIONS DE LA RESISTANCE AU FLAMBEMENT

La résistance au flambement d'un élément ou d'un composant de section, peut être améliorée de plusieurs façons.

Pour une forme de flambement donnée, une réduction du rapport d'élancement se traduira par une charge ultime plus élevée. Ceci sera normalement réalisé en augmentant les dimensions de la section droite ; cela peut aussi être fait en répartissant le matériau de manière différente le long du centre de gravité, tout en gardant à la section droite une section constante ; en faisant cela, cependant, on peut changer la réponse de la section et/ou de l'élément, de telle sorte que d'autres formes de flambement puissent devenir critiques. En particulier, une diminution d'épaisseur de composants de section droite, afin de mieux répartir le matériau, a souvent pour conséquence un voilement, prépondérant d'un point de vue calcul.

Une autre manière d'améliorer la résistance au flambement d'un élément est de lui fournir des maintiens de meilleure qualité ou supplémentaires, afin de modifier le mode de flambement. La charge critique élastique d'un poteau en compression axiale biarticulé, par exemple, est augmentée d'un facteur 4 si on ajoute un appui simple à mi-hauteur, de telle sorte que le poteau flambe dans un mode en deux demi-ondes sinusoïdales. De la même manière une poutre simplement appuyée, soumise à de la flexion par rapport à son axe le plus fort, est renforcée vis-à-vis du déversement en empêchant les rotations de flexion et/ou de torsion à ses supports d'extrémités, ou, plus simplement, en mettant un obstacle à tout déplacement latéral de la semelle en compression au moyen d'un entretoisement adéquat. La résistance ultime d'une plaque mince comprimée peut être améliorée de façon appréciable en fixant des raidisseurs longitudinaux et éventuellement transversaux ; à condition qu'ils soient assez rigides, la plaque flambera entre les raidisseurs, pour une contrainte critique élastique plus élevée. Le fait de raidir des structures en coques produira, de la même manière, une augmentation de la résistance.

Bien que la résistance de calcul soit plutôt reliée à la contrainte ultime qu'à la contrainte critique élastique, les commentaires ci-dessus peuvent, qualitativement être étendus à la capacité porteuse ultime.

8.   INSTABILITE DE PORTIQUE

Quand on conçoit des poteaux comme des parties d'un portique, il peut être pratique d'isoler les poteaux du reste du portique et de traiter leur calcul comme des problèmes séparés. Cependant, la plupart des poteaux appartenant à des portiques de bâtiments subissent des actions de flexion appliquées à leurs extrémités, en plus des efforts normaux. Ces actions de flexion dépendent de l'interaction entre le poteau et ses éléments adjacents - poutres et poteaux. Dans certains cas, le poteau soutiendra les poutres à l'effondrement ; de telles situations se présentent quand les poutres sont conçues en plasticité et s'effondrent quand le poteau reste stable et élastique. Il y a d'autres situations où les poutres supportent le poteau ; c'est en particulier le cas quand les poutres sont conçues en élasticité et présentent un comportement élastique jusqu'à la ruine, cette dernière étant amorcée par l'instabilité du poteau.

La plupart du temps, les poteaux de portique apparaîtront comme des éléments encastrés de manière élastique, soumis à des efforts normaux et des couples d'extrémités combinés. On les appelle alors « éléments comprimés fléchis » (ou encore « poutres-colonnes » en Belgique ou en Suisse).

Dans la plupart des portiques de bâtiment, les déplacements d'ossature sont empêchés par des dispositifs de contreventement appropriés, par exemples des entretoises sur les façades, des escaliers, un noyau central en béton armé pour les réseaux en tous genres. Ensuite les extrémités du poteau doivent éviter de subir des déplacements horizontaux. La stabilité d'ossatures rigides se ramène à la stabilité de ses poteaux individuels. Il est donc nécessaire d'avoir des règles appropriées concernant la résistance ultime d'éléments élastiques en compression maintenus soumis à des moments d'extrémités supplémentaires.

Quelquefois des forces horizontales, dues au vent et à des séismes éventuels doivent être équilibrées par des actions de flexion sur le portique tout entier qui présente des déplacements horizontaux, augmentant la plupart du temps de la base au sommet. Ensuite les poteaux se déforment selon une forme en S, appelée flexion à double courbure. Les déplacements horizontaux permettent aux efforts dus aux poids propres de développer des moments fléchissants supplémentaires, appelés souvent moments secondaires car ils résultent de charges de poids qui agissent sur le portique déformé. Le terme secondaire est particulièrement mal adapté parce la grandeur de ces moments fléchissants secondaires peut rarement être négligée. Vérifier la stabilité du portique en considérant la stabilité des poteaux individuels apparaît alors plus comme une recette de cuisine que comme une procédure de calcul réfléchie, mais constitue une tentative de prise en compte de l'influence des effets du second ordre dans la structure en portique.

9.   CONCLUSION

·      Les manières les plus efficaces d'améliorer la résistance au flambement consistent à accroître les dimensions de la section droite et/ou d'utiliser un contreventement et des maintiens de manière à modifier le mode de flambement.

·      La stabilité d'un portique à ossature rigide est contrôlée par la stabilité de ses poteaux individuels.

·      La stabilité d'un portique à ossature souple est contrôlée par la rigidité de flexion des poteaux et des poutres et par la rigidité des liaisons poutres/poteaux.

10. LECTURES COMPLEMENTAIRES

1.           Ballio, G. et Mazzolani, F., "Theory and Design of Steel Structures", Chapman and Hall, London, 1983.

2.           Dowling, P.J., Knowles, P. et Owens, G.W., "Structural Steel Design", Butterworths, London, 1988.

3.           Galambos, T.V. (éditeur), "Guide to Stability Design Criteria for Metal Structures", John Wiley and Sons, New York, 1988.

4.           McGuire, W., "Steel Structures", Prentice-Hall Inc. , Englewood Clifs, N.J., 1988.

5.           Picard, A. et Beaulieu, D., "Calcul des charpentes en acier", Institut Canadien de la Construction en Acier, 1991.

6.           CECM Recommendations of Steel Shells, Publication CECM n° 56, 1988.