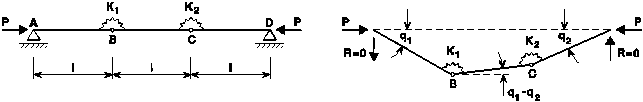
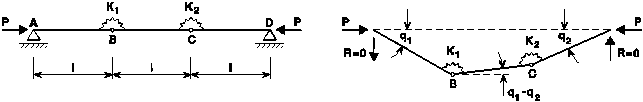
l = P
AB, BC et CD sont des barres rigides liées par des ressorts
de rotation avec rigidités K1, K2. Le système possède
deux degrés de liberté : q1, q2.
En admettant que q1 sont q2 sont petits (sin q1 » q1, sin q2 » q2, cos q1 » 1, cos q2 » 1), les équations d'équilibre :
|
S MB = 0
K1 (2q1 - q2) - P S MC = 0
K2 (2q2 - q1) - P conduisent au système d'équations suivant, écrit sous forme matricielle :
|
|
La procédure itérative correspondante est :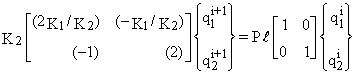 
où les termes de droite représente les sollicitations (moments fléchissants en B et C).
Après chaque itération, en égalisant {q}i+1 à {q}i il est possible d'obtenir une limite inférieure, une limite supérieure et une estimation de la charge critique Pcr.
La limite supérieure (inférieure) de Pcr est la
plus grande (petite) valeur de P qu'il faut multiplier par une composante de
qi+1 pour égaliser la composante correspondante de qi,
i.e. pour faire qi+1 /qi = 1. L'estimation de 
est
la moyenne des valeurs de P nécessaires pour rendre égales les paires de composantes
correspondantes de qi et qi+1.
|
i |
{q}i |
Efforts (x P |
{q}i+1 (x P |
{q}i+1 /{q}i (x P |
Limite inférieure (x K/ |
Limite supérieure (x K/ |
Estimation (x K/ |
|
1 |
|
|
|
|
0 |
1,5 |
0,75 |
|
2 |
|
|
|
|
0,75 |
1,2 |
0,975 |
|
3 |
|
|
|
|
0,923 |
1,071 |
0,997 |
soit : 0,923 
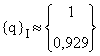Résultats exacts : 
|
i |
{q}i |
Efforts (x P |
{q}i+1 (x P |
{q}i+1 /{q}i (x P |
Limite inférieure (x K/ |
Limite supérieure (x K/ |
Estimateur (x K/ |
|
1 |
|
|
|
|
0 |
1,5 |
- |
|
2 |
|
|
|
|
0,5 |
1 |
0,75 |
|
3 |
|
|
|
|
0,6 |
0,75 |
0,675 |
soit : 0,6 
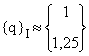Résultats exacts : 
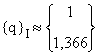
La charge de bifurcation critique d'un poteau comprimé avec conditions d'appui arbitraires est la valeur propre la plus petite du problème de valeurs et fonctions propres suivant :
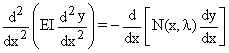(1)
où l’on admet que l'effort axial N dépend d'un seul paramètre de charge l. Ici, on ne considère que des problèmes dans lesquels N est constant par tronçons, ce qui veut dire que l'équation (1) devient :
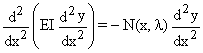(2)
L'équation (2) est équivalente
à :
(3)
où le moment fléchissant M(x, l) est donné par :
M(x,
l) = N(l) y (x) + A(l) x + B(l) (4)
et les valeurs de A(l) et B(l) peuvent être déterminées à partir des conditions d'appui.
On doit remarquer que l'application de la méthode de Vianello oblige à calculer M(x, l) à chaque itération (étape (ii)) ce qui peut demander un effort considérable (particulièrement dans le cas de poteaux hyperstatiques). Ici, avec le but d’illustrer l'application de la méthode de Vianello à un système continu, on se limite au cas très simple d'un poteau biarticulé soumis à une compression uniforme.
Comme, dans ce cas, A(l) = B(l) =
0, l'équation différentielle d'équilibre est donnée par 
et
conduit à la procédure itérative 
.
On choisit comme estimation initiale de la configuration déformée
du poteau y1 (x) = 
en remarquant
qu'elle doit vérifier les conditions aux limites cinématiques : y1
(0) = y1 (L) = 0.
Puis on multiplie cette estimation initiale par P, pour obtenir les moments fléchissants correspondants. Intégrant deux fois et imposant les conditions d'appui, on est conduit à :
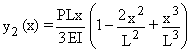
Puis, on définit :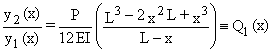 
En égalisant [Q1(x)]max et [Q1(x)]min à l'unité, on obtient des limites supérieure et inférieure de la charge critique Pcr :
Pour calculer des estimations de la charge critique, il faut, avant tout, définir un « critère de similarité » entre y1 (x) et y2 (x). Deux critères possibles sont :
(a) Égaliser les valeurs moyennes :
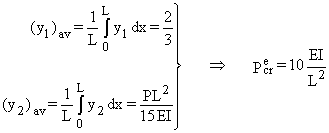
(b) Égaliser y1 (L/2) et y2 (L/2) :
y1 (L/2) = 1 et
La répétition de la procédure avec l'estimation initiale :
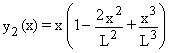(configuration identique au résultat de l'itération 1)
conduit à :
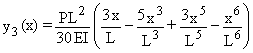
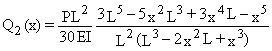
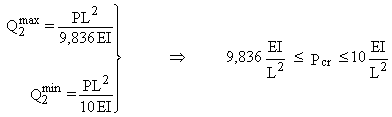
(a) (y2)av
= (y3)av 
(b) y2
(L/2) = y3 (L/2) 
Estimation du mode d'instabilité :
Résultats exacts : 
=
9,8696 
q1
= 0
q2
= 0
)
/3K)
/3K)
)
)
)
)
/3K)
/3K)
)
)
)
