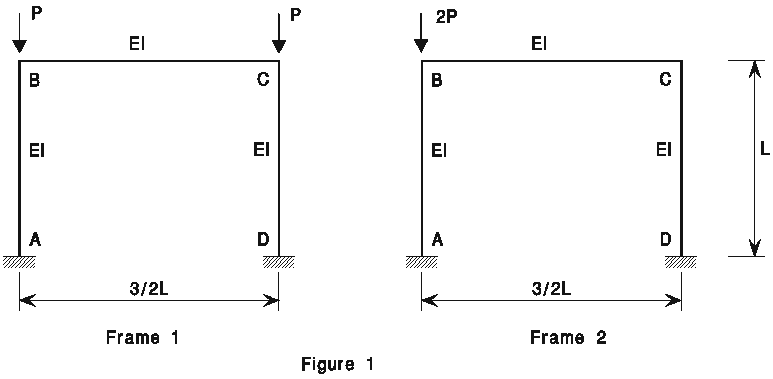
EXEMPLE 6 (ii) : Calcul de la charge critique de portiques simples a nœuds fixes ou nœuds déplaçables
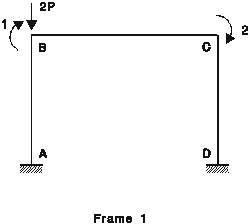
On considère les deux portiques simples représentés à la figure 1.

a) Calculer exactement les valeurs de la charge critique de chacun des portiques
a1) Avec nœuds fixes
a2) Avec nœuds déplaçables
b) Calculer approximativement les valeurs de la charge critique de chacun des portiques en utilisant la méthode des éléments finis
b1) Avec nœuds fixes
b2) Avec nœuds déplaçables
c) Quelles conclusions peuvent être tirées en comparant les valeurs des charges critiques des deux portiques avec nœuds fixes et déplaçables?
a) Quoique les valeurs exactes de la charge critique Pcr soient ici déterminées au moyen de l'équation différentielle, il faut dire que cette méthode n'est pas la plus efficace pour faire ce travail. En particulier, il existe une méthode basée sur l'emploi d'une matrice de rigidité non linéaire qui est beaucoup plus efficace. Cependant, l'utilisation de cette matrice de rigidité présente le désavantage d'engager le concept de fonctions de stabilité, lequel n'a pas encore été introduit.
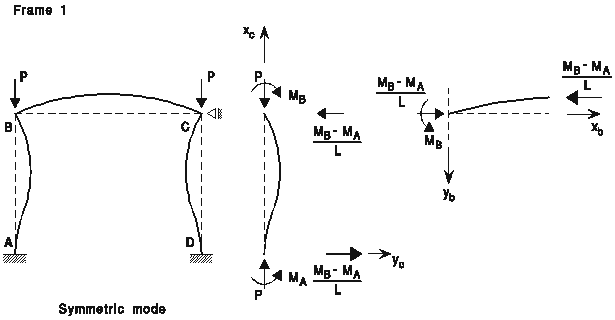
EI y"c + Pyc = MA
+ ![]() xc
() " º
xc
() " º ![]()
yc (0) =0
y¢c (0) =0 yc
(L) = 0
() ¢ º ![]()
La solution générale est : yc = A
sin Kc xc + B cos Kc xc +
![]() xc
+
xc
+ ![]() Kc2 =
Kc2 = ![]()
En introduisant les conditions aux limites on obtient :
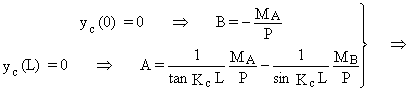
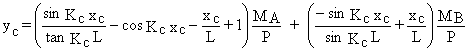
y¢c
(0) =0 Þ
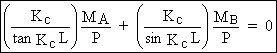 (1)
(1)
Poutre BC (en négligeant l'influence de l'effort axial)
EI y²b = MB yb
= Cxb + D + ![]()

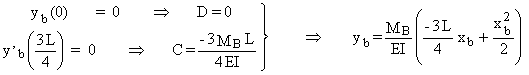
y¢c (L) = y¢b
(0) Þ =
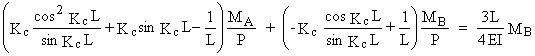
Þ
![]()
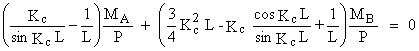 (2)
(2)
Le système formé par les équations (1) et (2) est (PL sin Kc L ¹ 0) :
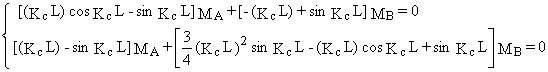
Þ MA = MB = 0 ou
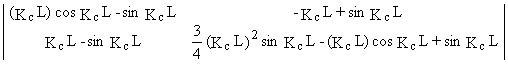 = 0
= 0
La plus petite racine de l'équation caractéristique :
![]()
est KcL » 4,877, ce qui correspond à : ![]()
yc =
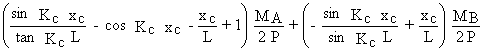
y¢c (0) =0 Þ
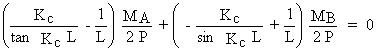 Kc2 =
Kc2 =
![]() (1)
(1)
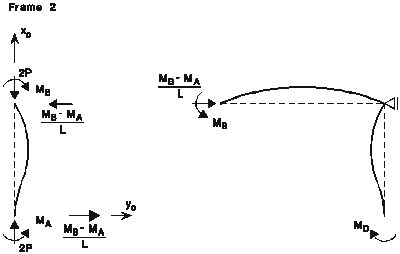
Portique BCD (en négligeant l'influence de l'effort axial)
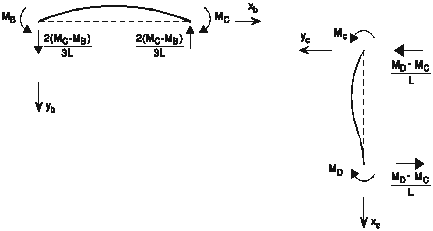
E I y²c = MC
+ ![]() xc yc = C
xc + D +
xc yc = C
xc + D + ![]()
![]()
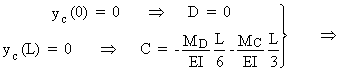
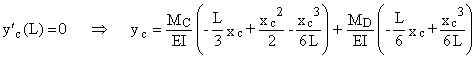
y¢c
(L) = 0 Þ
![]()
MD = 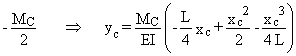
EIy²b = MB
+ ![]() yb
= C xb + D +
yb
= C xb + D + 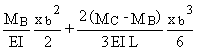
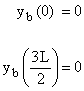
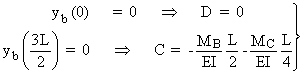
Þ
yb = 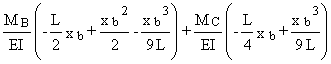
y¢b
![]()
Þ
MC = 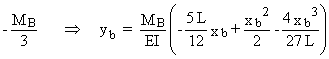
y¢c (L) = y¢b
(0) Þ 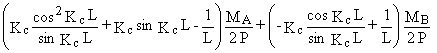 =
=
![]()
Þ
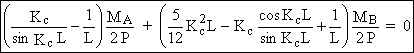 (2)
(2)
Le système formé par les équations (1) et (2) est (PL sin Kc L ¹ 0) :
Þ MA = MB = 0
ou
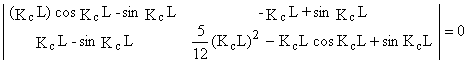
La plus petite racine de l'équation caractéristique :
![]()
est KcL » 5,095, ce qui correspond à : ![]()
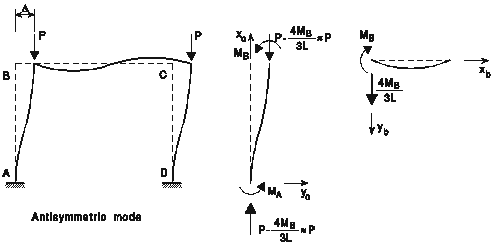
Poteau
AB (admettant P - ![]() »
P)
»
P)
EIy²c
+ Pyc = MA
yc = A sin Kc xc + B cos Kc xc
+ ![]()
yc (0)
= 0 yc
(L) = D yc
(0) = 0 Þ B = ![]() Kc2
=
Kc2
= ![]()
y¢c
(0) = 0 yc
(L) = D Þ A = 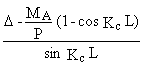
PD = MA + MB Þ
D = ![]() Þ
yc =
Þ
yc = 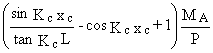 +
+
![]()
y¢c
(0) = 0 Þ
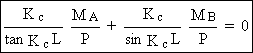 (1)
(1)
EIy²b
= ![]() xb
- MB yb
= C xb + D +
xb
- MB yb
= C xb + D + ![]()
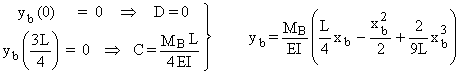
y¢c (L) =
y¢b (0) Þ
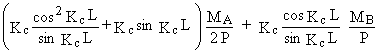 =
=
![]()
Þ
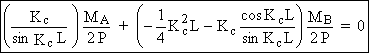 (2)
(2)
Le système formé par les équations (1) et (2) est (PL sin Kc L ¹ 0) :
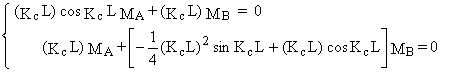
Û MA = MB
= 0 ou
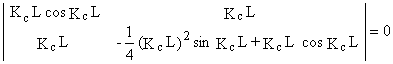
La plus petite racine de l'équation caractéristique : 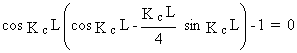
est KcL » 2,5715, ce qui correspond à :
![]()
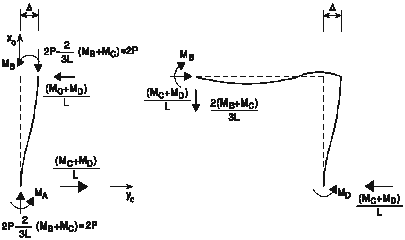
Poteau
AB (en admettant que ![]() )
)
EIy²c + 2 P y
c = MA + ![]()
![]() Kc2
=
Kc2
= ![]()
yc (0) = 0 Þ
B = - ![]()
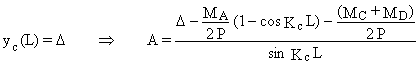
yc¢ (0) = 0
![]()
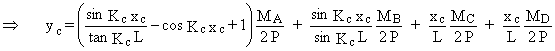
yc¢
(0) = 0 Þ
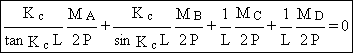 (1)
(1)
Portique
BCD (en admettant que ![]() dans le
poteau CD et en négligeant l'influence de l'effort axial dans le comportement
de la poutre BC)
dans le
poteau CD et en négligeant l'influence de l'effort axial dans le comportement
de la poutre BC)
![]()
E I yc² = MC - ![]()
![]()
yc (0) = - D = - ![]()
![]()
![]()
![]()
yc¢ (L) = 0
yc
= 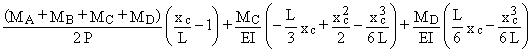
yc¢
(L) = 0 Þ ![]()
Þ
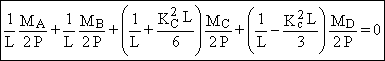 (2)
(2)
E I yb² = - MB + ![]()
![]() yb
(0) = 0 Þ D
= 0
yb
(0) = 0 Þ D
= 0
![]()
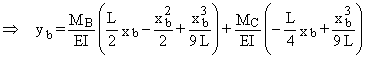
![]()
![]()
Þ
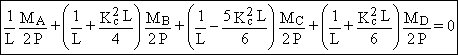 (3)
(3)
yc¢ (L) = y¢b
(0) Þ
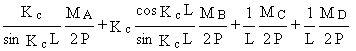 =
= ![]()
Þ
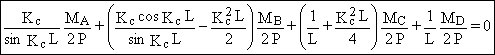 (4)
(4)
Le système formé par les équations (1), (2), (3) et (4) est (PL sin Kc L ¹ 0)
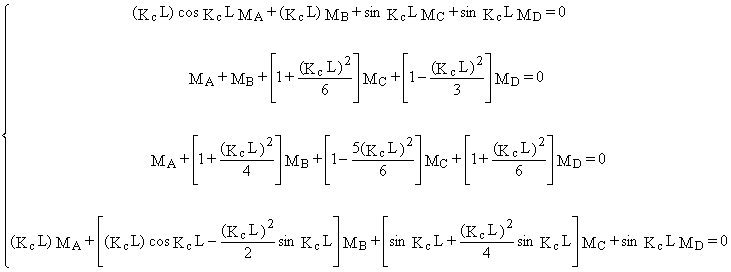
|
Û MA = MB = MC= MD = 0or |
Kc L cos Kc L |
Kc L |
sin Kc L |
sin Kc L |
= 0 |
|
1 |
1 |
|
|
||
|
1 |
|
|
|
||
|
Kc L |
|
|
|||
La plus petite racine de l'équation caractéristique est Kc L »
3,6149, ce qui correspond à : ![]()
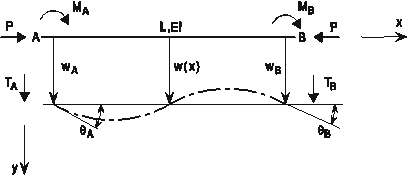
d2 V = d2 U + d2 W
d2 U =
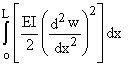
d2
W = 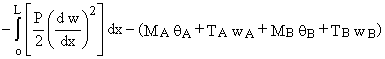
wa = w(0)
wB = w(L)
qA = ![]() qB =
qB = ![]()
w (x) = q1 x3 + q2 x2 + q3 x + q4 fonction de déplacement approchée
Exprimant les constants q1, q2, q3, q4 en fonction des déplacements des nœuds wA, qA, wB, qB, on est conduit à :
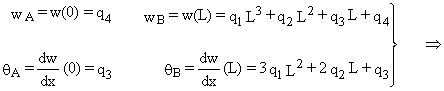
q1 = ![]()
q2 = ![]()
q3 = qA q4 = wA
et à une nouvelle expression pour la fonction de déplacement approchée, écrite maintenant en termes des déplacements des nœuds :
w (x) = 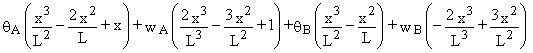 º Q1
i1 (x) + Q2 i2 (x)
+ Q3 i3 (x) + Q4 i4
(x)
º Q1
i1 (x) + Q2 i2 (x)
+ Q3 i3 (x) + Q4 i4
(x)
alors, on a :
d2 V= ![]() [Kij
+ Gij ] Qi Qj - Fi Qi
(i,j = 1,4)
[Kij
+ Gij ] Qi Qj - Fi Qi
(i,j = 1,4)
où : Kij = EI 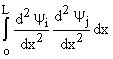 éléments de la matrice de rigidité linéaire (premier ordre).
éléments de la matrice de rigidité linéaire (premier ordre).
Gij = - P 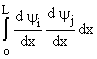 éléments de la matrice de rigidité géométrique.
éléments de la matrice de rigidité géométrique.
Pour assurer l'équilibre, il est alors nécessaire d’avoir :
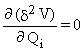 Þ [Kij
+ Gij ] Qj - Fi = 0 Þ
Fi = [Kij + Gij ] Qj
Þ [Kij
+ Gij ] Qj - Fi = 0 Þ
Fi = [Kij + Gij ] Qj
![]()
Sous forme matricielle :
![]()

![]()

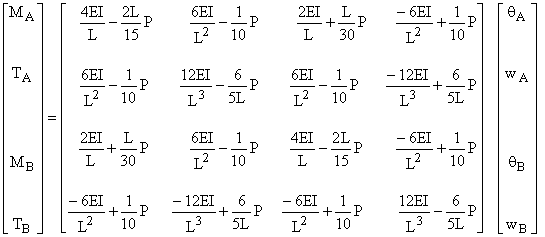
Il faut noter que :
(i) Cette matrice de rigidité approchée peut aussi être obtenue en linéarisant la matrice de rigidité exacte, laquelle est écrite en termes des fonctions de stabilité.
(ii) Si P = 0, cette matrice de rigidité est exacte. Donc, il ne faut considérer qu'un élément fini par barre.
(iii) Si P ¹ 0, cette matrice de rigidité est approchée. Cependant, on peut montrer qu'il ne faut jamais considérer plus que trois éléments finis par barre pour obtenir des résultats pratiquement exacts (souvent, il suffit même de considérer seulement un ou deux éléments par membre).
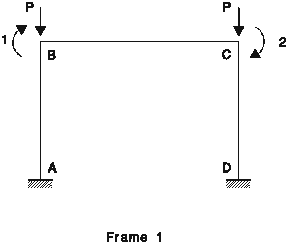
1 élément par poteau Q1 º qB Q2 º qC
K11 = ![]()
K22 = ![]() K12 = K21 =
K12 = K21 = ![]() l =
l = ![]()
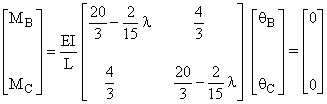
Û qB = qC = 0 ou
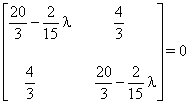
La plus petite racine de l'équation caractéristique est l = 40,
ce qui conduit à : ![]()
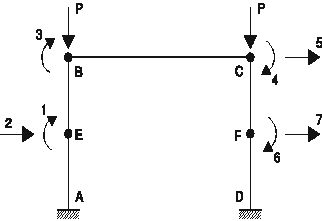
2 éléments par poteau
Q1 = qE Q2 = wE/ (L/2) Q3 = qB Q4 = qC
Q5 = qF
Q6 = wF / (L/2) l
= ![]()
K11 = K55 = ![]() K12 = K56 = 0 K13
= K45 =
K12 = K56 = 0 K13
= K45 = ![]()
K14 = K15 = K16 = K35 = K25
= 0 K22 = K66
= ![]() K34 =
K34 =
![]()
K23 = K46 = ![]() K24 = K26 = K36 = 0
K33 = K44 =
K24 = K26 = K36 = 0
K33 = K44 = ![]()
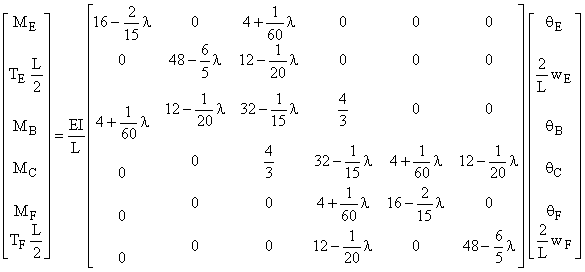
La plus petite racine de l'équation caractéristique est l = 24,343,
ce qui conduit à : ![]()
1 élément dans le poteau AB
Q1 = qB
Q2 = qC
l = ![]()
K11 = ![]() K12 =
K12 = ![]() K22 =
K22 = ![]()
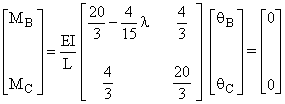
La racine de l'équation caractéristique est l = 24, ce qui conduit
à : ![]()
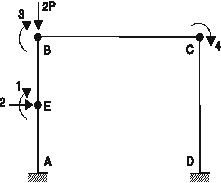
2 éléments dans le poteau AB
Q1 = qE
Q2 = wE/ (L/2) Q3
= qB Q4
= qC
l = ![]()
K11 = ![]() K12 = 0 K13 =
K12 = 0 K13 =
![]() K14 = 0
K14 = 0
K22 = ![]() K23 =
K23 = ![]() K24 = 0 K34
=
K24 = 0 K34
= ![]()
K33 = ![]() K44 =
K44 = ![]()
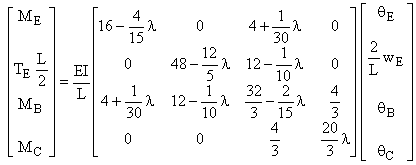
La plus petite racine de l'équation caractéristique est l = 13,265,
ce qui conduit à : ![]()
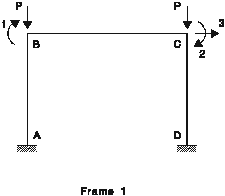
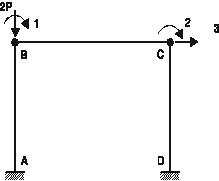
1 élément par poteau
Q1 º qB
Q2 º qC
Q3 = ![]() l =
l = ![]()
K11= ![]() K12 =
K12 = ![]() K13 =
K13 = ![]()
K22= ![]() K23 =
K23 = ![]() K33 =
K33 = ![]()
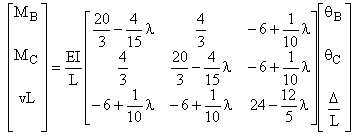
La plus petite racine de l'équation caractéristique est l = 6,667,
ce qui conduit à : ![]()
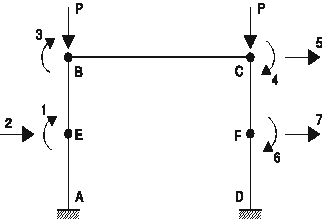
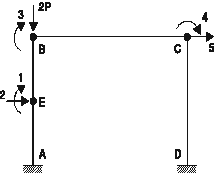
2 éléments par poteau
Q1 = qE Q2 = wE/ (L/2) Q3 = qB Q4 = qC Q5 = D/ (L/2)
Q6 = qF
Q7 = wF / (L/2) l
= ![]()
K11 = K66 = ![]() K12 = K67 = 0 K13
= K46 =
K12 = K67 = 0 K13
= K46 = ![]() K14 = 0
K14 = 0
K15 = K56 =
![]() K16 = K17 = 0 K22 = K77 =
K16 = K17 = 0 K22 = K77 =
![]()
K23 = K47 = ![]() K24 = K37 = 0 K25
= K57 =
K24 = K37 = 0 K25
= K57 = ![]()
K26 = K27 = 0 K33
= K44 = ![]() K34 =
K34 = ![]()
K35 = K45 = ![]() K36 = K37 = 0 K55
=
K36 = K37 = 0 K55
= ![]()
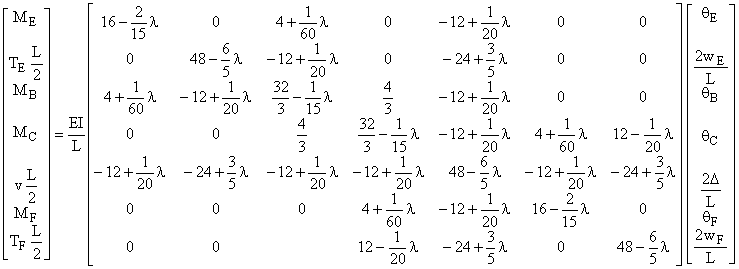
La plus petite racine de l'équation caractéristique est l = 6,622,
ce qui conduit à : ![]()
1 élément dans le poteau AB
Q1 = qB
Q2 = qC
Q3 = ![]()
K11 = ![]() K12 =
K12 = ![]() K13 =
K13 = ![]()
K22 = ![]() K23 =
K23 = ![]()
K33 = ![]()
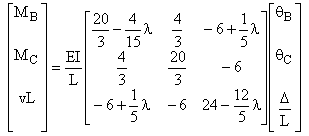
La racine de l'équation caractéristique est l = 6,667, ce qui
correspond à : ![]()
2 éléments dans le poteau AB
Q1 = qE Q2 = wE/ (L/2) Q3 = qB Q4 = qC Q5 = D/ (L/2)
K11 = ![]() K12
= 0 K13 =
K12
= 0 K13 = ![]() K14 = 0 K15 =
K14 = 0 K15 =
![]()
K22 = ![]() K23 =
K23 = ![]() K24 = 0 K25 =
K24 = 0 K25 =
![]()
K33 = ![]() K34 =
K34 = ![]() K35 =
K35 = ![]()
K44 = ![]() K45 =
K45 = ![]()
K55 = ![]()
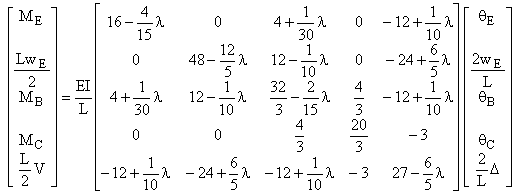
La plus petite racine de l'équation caractéristique est l = 6,557,
ce qui conduit à : ![]()
(i) Empêcher les déplacements latéraux des nœuds conduit, pour les deux portiques, à une croissance significative de la charge critique correspondante Pcr.
PORTIQUE 1 : Pcr
= 6,613 ![]() Þ Pcr
= 23,785
Þ Pcr
= 23,785 ![]() PORTIQUE 2 : Pcr = 6,534
PORTIQUE 2 : Pcr = 6,534 ![]() Þ
Pcr = 12,979
Þ
Pcr = 12,979 ![]()
(ii) Dans le cas des portiques à nœuds fixes, un changement de la distribution des forces verticales (la somme des deux forces est maintenue constante) fait varier significativement la valeur de la charge critique Pcr.
PORTIQUE 1 : Pcr
= 23,785 ![]() PORTIQUE 2 : Pcr = 12,979
PORTIQUE 2 : Pcr = 12,979 ![]()
(iii) Dans le cas des portiques à nœuds déplaçables, un changement de la distribution des forces verticales (la somme des deux forces est maintenue constante) ne fait presque pas varier la valeur de la charge critique Pcr.
PORTIQUE 1 : Pcr
= 6,613 ![]() PORTIQUE 2 : Pcr = 6,534
PORTIQUE 2 : Pcr = 6,534 ![]()
(iv) L'utilisation de la méthode des éléments finis avec un élément de barre comprimée a conduit à des résultats assez précis pour les portiques à nœuds déplaçables et très pauvres pour les portiques à nœuds fixes. La considération de deux éléments par barre comprimée a conduit à d'excellents résultats dans tous les cas (pratiquement exacts pour les portiques à nœuds déplaçables et avec des erreurs très petites pour les portiques à nœuds fixes)