EXEMPLE 6.1 (i) : CALCUL DE LA CHARGE CRITIQUE ET DE SON MODE D'INSTABILITÉ
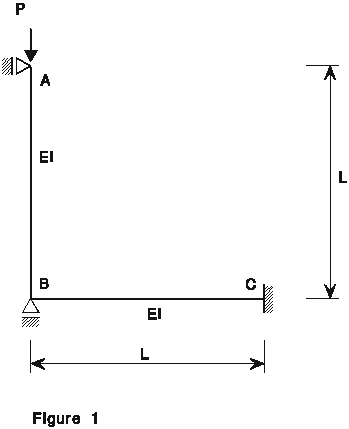
Déterminer la charge critique et le mode d'instabilité correspondant pour le poteau AB de la structure représentée à la figure 1 :

a) Exactement
b) Approximativement
b1) En utilisant la méthode du coefficient
de Rayleigh avec une configuration du mode d'instabilité donnée par : w(x) = q sin
![]()
b2) En utilisant la méthode de Rayleigh-Ritz
avec une configuration du mode d'instabilité donnée par : ![]()
b3) En utilisant la méthode de Galerkin avec la même configuration du mode d'instabilité qu’en b2).
b4) En utilisant la méthode de Vianello-Newmark avec la configuration du mode d'instabilité obtenue en b2) comme approximation initiale (considérer 4 éléments dans le poteau et faire une seule itération).
NOTE : Résoudre le problème aux valeurs et vecteurs propres obtenus en b2) et b3) en utilisant une méthode itérative et une méthode analytique.
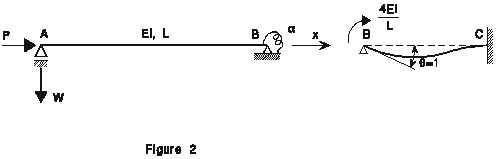
Pour déterminer la charge critique et le mode d'instabilité correspondant pour
le poteau AB, on adopte un modèle structural dans lequel la poutre BC est remplacée
par un ressort de rotation avec une rigidité a = ![]() (figure
2).
(figure
2).
a) L'équation différentielle qui décrit le flambement d'un poteau avec des conditions d'appui arbitraires est donnée, pour le cas d’une rigidité en flexion EI et d’un effort de compression P par :
![]() (1)
(1)
(voir, par exemple, Timoshenko, S.P., “Theory of Elastic Stability”, McGraw Hill, New York, 1960).
La solution générale de cette équation différentielle est :
w = A sin kx + B cos kx + Cx + D où : k2
= ![]() (2)
(2)
Dans ce problème particulier, les conditions d'appui lesquelles permettent la détermination des valeurs des coefficients A, B, C, D sont :
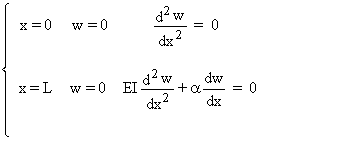 (3)
(3)
Introduisant les conditions (3) dans l'équation (2), on obtient :
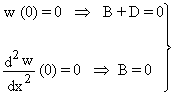 Þ
Þ ![]()
w (L) = 0 Þ A sin kL + CL = 0 Þ
![]()
![]()
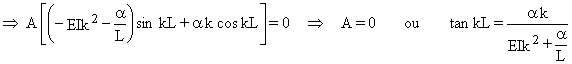
a = ![]() Þ
Þ
![]() (4)
(4)
La plus petite racine de l'équation (4) est kL = 3,8289, ce qui correspond à la valeur de la charge de bifurcation critique Pcr :
![]() = 3,8289 Þ
= 3,8289 Þ
![]()
Le mode d'instabilité associé à la charge de bifurcation critique est :
w (x) = A ![]() avec : k
=
avec : k
= ![]()
c’est-à-dire :
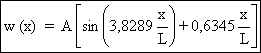
La variation de l'énergie potentielle du poteau est donnée par : d2U = d2U + d2 W
où : d2U = 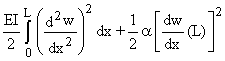 est l'énergie de déformation correspondante au mode d'instabilité
est l'énergie de déformation correspondante au mode d'instabilité
et d2 W =
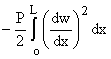 est la variation du potentiel de la charge appliquée P.
est la variation du potentiel de la charge appliquée P.
b1) En considérant que, dans ce cas,
w (x) = q sin ![]() ,
,
![]() ,
,
![]()
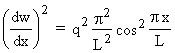 ,
,
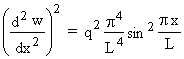 ,
,
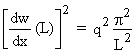
avec :
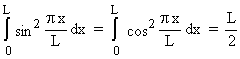
on obtient, pour d2U et d2
W : d2U
= EI 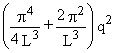 ; d2
W =
; d2
W = ![]()
La valeur approchée de la charge critique est, alors :
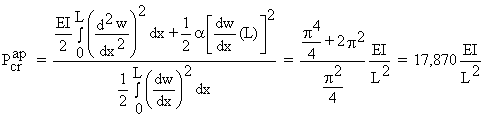
![]() ,
,
![]()
b2) En considérant que, dans ce cas, :
w (x) = q1 sin ![]()
![]() = q1
= q1
![]()
![]() =
= ![]()
![]() =
= 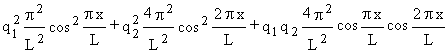
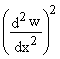 =
= 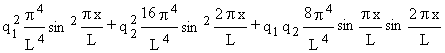
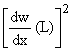 =
= 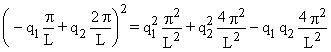
et avec : 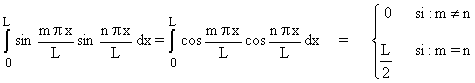
on obtient, pour d2 V :
d2V=
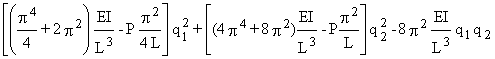
L'équilibre est alors assuré si :
q1 = q2 = 0 ou
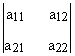 = 0
= 0
où : a11 =
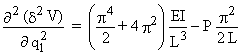 a12 = a21=
a12 = a21=
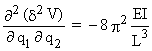
a22 = 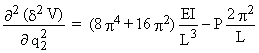
La plus petite racine de l'équation caractéristique a11.a22 - a122 = 0 est d'abord obtenue itérativement.
Définissant un paramètre de charge, l = ![]() , on a :
, on a :
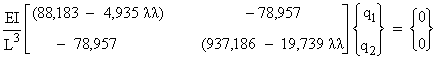
La procédure itérative donne :
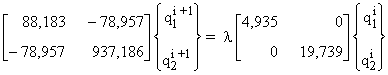
i) 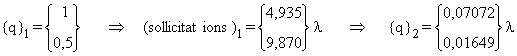
ii) 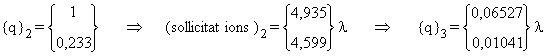
iii) 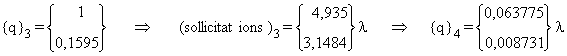
iv) 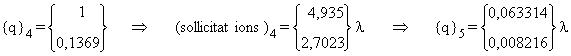
v) 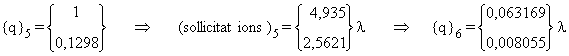
vi) 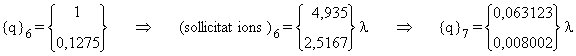
vii) 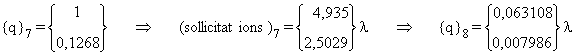
viii) 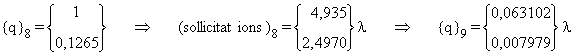
ix)
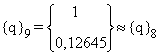
d’où :
![]()
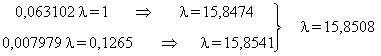 Þ
Þ
![]()
Analytiquement, la valeur propre plus petite est obtenue à partir de l'équation caractéristique : 97,412 l2 - 6365,657 l + 76409,665 = 0
comme l = 15,8463, ce qui correspond au vecteur propre : (88,183 - 4,935 ´ 15,8463) q1 - 78,957 q2 = 0 Þ q2 = 0,1265 q1
Par conséquent : ![]()
![]()
b3) Comme la configuration approchée du mode d'instabilité employée ne vérifie pas une des conditions aux limites statiques (moment fléchissant à x = L), l'utilisation de la méthode de Galerkin oblige à considérer un terme additionnel. Outre le résidu au long de la longueur du poteau, il est aussi nécessaire prendre en considération un résidu correspondant à la condition aux limites qui n'est pas vérifiée. Dans ce cas particulier, ce résidu doit être « pondéré » à travers les valeurs des dérivées des fonctions d'approximation (la rotation est le déplacement généralisé qui correspond au moment).
La valeur du résidu est :
Pour 0 < x < L
L [w (x) ] = ![]()
![]() =
= 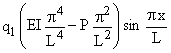 +
+ 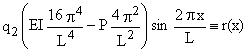
Pour x = L
B [w (x) ] = ![]()
![]()
L'utilisation de la méthode de Galerkin conduit alors à :
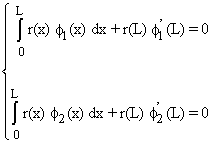
où : f1 (x) = sin
![]() f1¢ (x) =
f1¢ (x) = ![]() f2 (x) = sin
f2 (x) = sin ![]() f2¢ (x) =
f2¢ (x) = ![]()
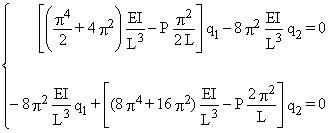
Ce système d'équations est précisément celui qui a été obtenu en b2). Cela veut dire que la solution sera la même :
Pcr£
15,8463 ![]() w
(x) = q1
w
(x) = q1 ![]()
On doit remarquer que les méthodes de Rayleigh-Ritz et Galerkin, utilisées avec les mêmes fonctions d'approximation pour le mode d'instabilité, conduisent toujours à des résultats identiques dans des problèmes conservatifs (structures élastiques soumises à des forces conservatives).
b4) Comme le poteau est hyperstatique, il est nécessaire d'utiliser la méthode des efforts. On obtient la structure base en supprimant le ressort de rotation de l'appui B.
Le choix initial de la configuration déformée est obtenu à partir de
![]() et consiste
en (figure 3) :
et consiste
en (figure 3) :
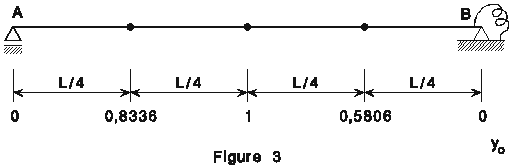
CALCUL DE LA FLEXIBILITÉ

|
0 |
0 |
0 |
0 |
V¢ |
|||||||
|
-1 |
-1 |
-1 |
-1 |
-1 |
M¢ |
||||||
|
1 |
0,75 |
0,5 |
0,25 |
0 |
Mcorr |
||||||
|
0 |
-0,25 |
-0,5 |
-0,75 |
-1 |
M |
||||||
|
0 |
-0,25 |
-0,5 |
-0,75 |
-1 |
|
c |
|||||
|
Discrétisation linéaire |
-0,25 |
-1,5 |
-3 |
-4,5 |
-2,75 |
|
cdisc |
||||
|
-0,25 |
-1,75 |
-4,75 |
-9,25 |
|
q¢ |
||||||
|
0 |
-0,25 |
-2 |
-6,75 |
-16 |
|
y¢ |
|||||
|
0 |
4 |
8 |
12 |
16 |
|
ycorr |
|||||
|
4 |
4 |
4 |
4 |
|
qcorr |
||||||
|
3,75 |
2,25 |
-0,75 |
-5,25 |
|
q |
||||||
|
0 |
3,75 |
6 |
5,25 |
0 |
|
y º
|
qB = - 5,25 ![]()
|
0 |
0,8336 |
1 |
0,5806 |
0 |
yo |
|||||
|
-0,8336 |
-0,1664 |
0,4194 |
0,5806 |
Dy |
||||||
|
1 |
1 |
1 |
1 |
P |
N |
|||||
|
-0,8336 |
-0,1664 |
0,4194 |
0,5806 |
P |
DM |
|||||
|
0 |
-0,8336 |
-1 |
-0,5806 |
0 |
P |
M¢ºM |
||||
|
0 |
-0,8336 |
-1 |
-0,5806 |
0 |
|
c |
||||
|
-4,0016 |
-18,672 |
-22,8284 |
-13,612 |
-2,4836 |
|
cdisc |
||||
|
-4,0016 |
-22,6736 |
-45,502 |
-59,114 |
|
q¢ |
|||||
|
0 |
-4,0016 |
-26,6752 |
-72,1772 |
-131,2912 |
|
y¢ |
||||
|
0 |
32,8228 |
65,6456 |
98,4684 |
131,2912 |
|
ycorr |
||||
|
32,8228 |
32,8228 |
32,8228 |
32,8228 |
|
qcorr |
|||||
|
28,8212 |
10,1492 |
-12,6792 |
-26,2912 |
|
q |
|||||
|
0 |
28,8212 |
38,9704 |
26,2912 |
0 |
|
y |
qB = -26,2912 ![]()
![]()
y1 = y + MB = y - 0,5138 P ![]()
|
0 |
21,1142 |
26,6392 |
15,5014 |
0 |
|
y1 |
|
- |
25,3289 |
26,6392 |
26,6989 |
- |
|
y1 /y0 |
soit :
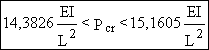
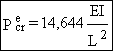
|
0 |
0,7926 |
1 |
0,5819 |
0 |
w (x) |
|
0 |
0,7755 |
1 |
0,5899 |
0 |
Calcul exact |